(本小题满分14分)
若a、b、c是△ABC三个内角A、B、C所对边,且 ,
,
(1)求 ;(2)当
;(2)当 时,求
时,求 的值。
的值。
(本小题15分)
如图在三棱锥P-ABC中,PA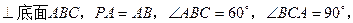
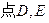 分别在棱
分别在棱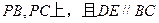 ,
,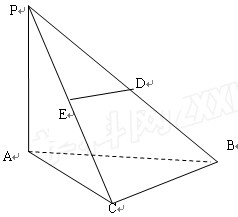
(1)求证:BC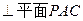
(2)当D为PB中点时,求AD与平面PAC所成的角的余弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角,并说明理由。
(本小题15分)
已知函数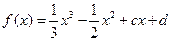 有极值.
有极值.
(1)求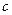 的取值范围;
的取值范围;
(2)若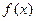 在
在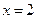 处取得极值,且当
处取得极值,且当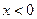 时,
时,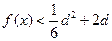 恒成立,求
恒成立,求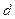 的取值范围.
的取值范围.
(本小题14分)
如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,
平面VAD
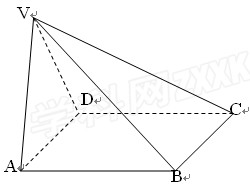
(1)证明:AB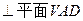 ;
;
(2)求面VAD与面VDB所成的二面角的余弦值。
(本小题14分)
已知函数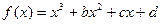 的图像过点
的图像过点 ,且在点
,且在点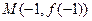 处的切线方程为
处的切线方程为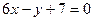 ,
,
(1)求函数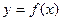 的解析式;
的解析式;
(2)求函数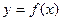 的单调区间。
的单调区间。
(本小题14分)
设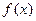 是定义在
是定义在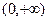 上的单调增函数,满足
上的单调增函数,满足 ,
,
(1)求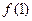 ;
;
(2)若 ,求
,求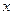 的取值范围。
的取值范围。