(本小题满分12分)△ABC中,角A、B、C对边分别是a、b、c,满足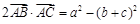 .
.
(Ⅰ)求角A的大小;
(Ⅱ)求 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
(本小题满分14分)已知函数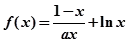
(1)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数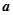 的取值范围;
的取值范围;
(2)讨论函数 的单调性;
的单调性;
(3)当 时,求证:对大于
时,求证:对大于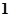 的任意正整数
的任意正整数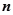 ,都有
,都有 。
。
(本小题满分13分)
在平面直角坐标系中,已知 ,若实数
,若实数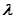 使得
使得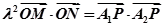 (
( 为坐标原点)
为坐标原点)
(1)求 点的轨迹方程,并讨论
点的轨迹方程,并讨论 点的轨迹类型;
点的轨迹类型;
(2)当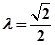 时,若过点
时,若过点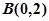 的直线与(1)中
的直线与(1)中 点的轨迹交于不同的两点
点的轨迹交于不同的两点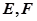 (
( 在
在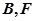 之间),试求
之间),试求 与
与 面积之比的取值范围。
面积之比的取值范围。
设集合W是满足下列两个条件的无穷数列{an}的集合:
①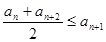 ②
② ,其中n∈N*,M是与n无关的常数
,其中n∈N*,M是与n无关的常数
(1)若{an}是等差数列,Sn是其前n项的和,a3=4,S3=18,试探究{Sn}与集合W之间的关系;
(2)设数列{bn}的通项为bn=5n-2n,且{bn}∈W,M的最小值为m,求m的值;
(3)在(2)的条件下,设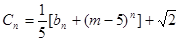 ,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
(本小题满分12分)如图,在直三棱柱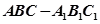 中,
中,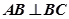 ,
,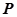 为
为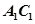 的中点,且
的中点,且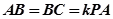 ,
,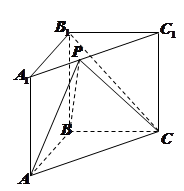
(1)当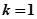 时,求证:
时,求证: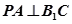 ;
;
(2)当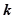 为何值时,直线
为何值时,直线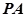 与平面
与平面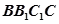 所成的角的正弦值为
所成的角的正弦值为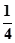 ,并求此时二面角
,并求此时二面角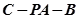 的余弦值。
的余弦值。