某中学校本课程共开设了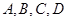 共
共 门选修课,每个学生必须且只能选修
门选修课,每个学生必须且只能选修 门选修课,现有该校的甲、乙、丙
门选修课,现有该校的甲、乙、丙 名学生.
名学生.
(Ⅰ)求这 名学生选修课所有选法的总数;
名学生选修课所有选法的总数;
(Ⅱ)求恰有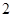 门选修课没有被这
门选修课没有被这 名学生选择的概率;
名学生选择的概率;
(Ⅲ)求 选修课被这
选修课被这 名学生选择的人数
名学生选择的人数 的分布列和数学期望.
的分布列和数学期望.
设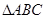 的内角
的内角 所对边的长分别为
所对边的长分别为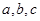 ,且
,且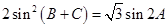 .
.
(Ⅰ)求 的度数;
的度数;
(Ⅱ)若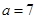 ,
, ,求
,求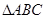 的面积
的面积 .
.
(本小题满分14分)设a为常数,且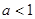 .
.
(1)解关于x的不等式 ;
;
(2)解关于x的不等式组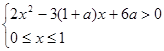 .
.
(本小题满分14分)如图,四棱柱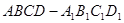 中,
中,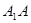 ^底面ABCD,且
^底面ABCD,且 . 梯形ABCD的面积为6,且AD//BC,AD=2BC,AB="2." 平面
. 梯形ABCD的面积为6,且AD//BC,AD=2BC,AB="2." 平面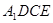 与
与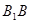 交于点E.
交于点E. 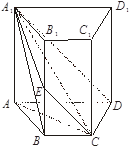
(1)证明:EC//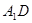 ;
;
(2)求点C到平面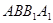 的距离.
的距离.
(本小题满分14分)某家电生产企业根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表:
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工时 |
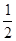 |
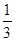 |
 |
| 产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)