本小题满分12分)
今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).
(Ⅰ)求水箱容积的表达式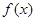 ,并指出函数
,并指出函数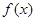 的定义域;
的定义域;
(Ⅱ)若要使水箱容积不大于 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.
已知函数 (1)求
(1)求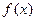 在区间
在区间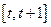 上的最大值
上的最大值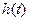 ;(2)若方程
;(2)若方程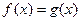 有且只有三个不同的实根,求实数
有且只有三个不同的实根,求实数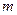 的取值范围.
的取值范围.
平面直角坐标系中,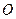 为坐标原点,给定两点
为坐标原点,给定两点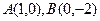 ,点
,点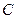 满足
满足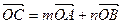 ,其中
,其中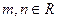 ,且
,且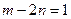 .(1)求点
.(1)求点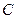 的轨迹方程;(2)设点
的轨迹方程;(2)设点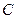 的轨迹与双曲线
的轨迹与双曲线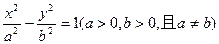 交于
交于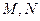 两点,且以
两点,且以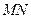 为直径的圆过原点,求证:
为直径的圆过原点,求证: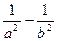 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于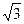 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
关于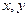 的方程
的方程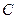 :
: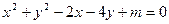 .(1)若方程
.(1)若方程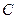 表示圆,求实数
表示圆,求实数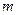 的范围;(2)在方程
的范围;(2)在方程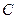 表示圆时,若该圆与直线
表示圆时,若该圆与直线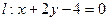 相交于
相交于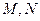 两点,且
两点,且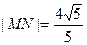 ,求实数
,求实数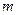 的值;(3)在(2)的条件下,若定点
的值;(3)在(2)的条件下,若定点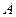 的坐标为(1,0),点
的坐标为(1,0),点 是线段
是线段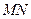 上的动点,求直线
上的动点,求直线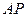 斜率的取值范围.
斜率的取值范围.
在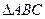 中,角
中,角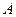 、
、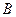 、
、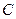 所对的边分别为
所对的边分别为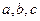 ,已知向量
,已知向量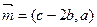
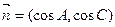 ,且
,且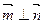 .(1)求角
.(1)求角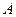 的大小;(2)若
的大小;(2)若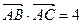 ,求
,求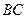 的最小值.
的最小值.
设函数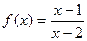 .
.
(1) 试根据函数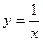 的图象平移
的图象平移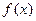 的图象,并写出交换过程;
的图象,并写出交换过程;
(2) 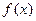 的图象是中心对称图形吗?
的图象是中心对称图形吗?
(3) 指出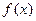 的单调区间
的单调区间