(本小题满分14分)
设函数 ,其中
,其中 .
.
( I )若函数 图象恒过定点P,且点P在
图象恒过定点P,且点P在 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当 时,设
时,设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设 ,曲线
,曲线 上是否存在两点P、Q,
上是否存在两点P、Q,
使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
已知函数f(x)=4cosωx·sin(ωx+ )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间[0, ]上的单调性.
]上的单调性.
已知α,β∈(0,π),且tanα=2,cosβ=-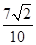 .
.
(1)求cos2α的值;
(2)求2α-β的值.
已知函数f(x)=- sin(2x+
sin(2x+ )+6sinxcosx-2cos2x+1,x∈R.
)+6sinxcosx-2cos2x+1,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在区间[0, ]上的最大值和最小值.
]上的最大值和最小值.
设函数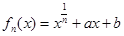
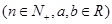 .
.
(1) 当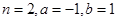 时,求函数
时,求函数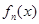 的极值;
的极值;
(2)若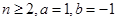 ,证明:
,证明: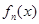 在区间
在区间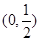 内存在唯一的零点;
内存在唯一的零点;
(3)在(2)的条件下,设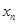 是
是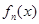 在区间
在区间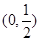 内的零点,判断数列
内的零点,判断数列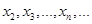 的增减性.
的增减性.
如图,已知椭圆 的右焦点为
的右焦点为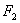 ,点
,点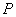 是椭圆上任意一点,圆
是椭圆上任意一点,圆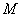 是以
是以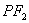 为直径的圆.
为直径的圆.
(1)若圆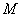 过原点
过原点 ,求圆
,求圆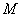 的方程;
的方程;
(2)写出一个定圆的方程,使得无论点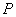 在椭圆的什么位置,该定圆总与圆
在椭圆的什么位置,该定圆总与圆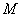 相切,请写出你的探究过程.
相切,请写出你的探究过程.