如图,已知椭圆 的右焦点为
的右焦点为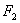 ,点
,点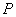 是椭圆上任意一点,圆
是椭圆上任意一点,圆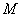 是以
是以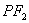 为直径的圆.
为直径的圆.
(1)若圆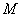 过原点
过原点 ,求圆
,求圆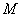 的方程;
的方程;
(2)写出一个定圆的方程,使得无论点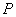 在椭圆的什么位置,该定圆总与圆
在椭圆的什么位置,该定圆总与圆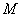 相切,请写出你的探究过程.
相切,请写出你的探究过程. 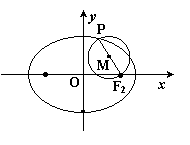
已知圆 .
.
(1)若直线 过点
过点 ,且与圆
,且与圆 相切,求直线
相切,求直线 的方程;
的方程;
(2)若圆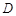 的半径为4,圆心
的半径为4,圆心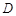 在直线
在直线 :
: 上,且与圆
上,且与圆 内切,求圆
内切,求圆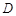 的方程.
的方程.
如图,斜四棱柱 的底面
的底面 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 ,
,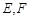 分别为
分别为 的中点.
的中点.
求证:(1)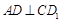 ;(2)
;(2) ∥平面
∥平面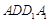 .
.
已知 为实数,
为实数, :点
:点 在圆
在圆 的内部;
的内部;  :
: 都有
都有 .
.
(1)若 为真命题,求
为真命题,求 的取值范围;
的取值范围;
(2)若 为假命题,求
为假命题,求 的取值范围;
的取值范围;
(3)若“ 且
且 ”为假命题,且“
”为假命题,且“ 或
或 ”为真命题,求
”为真命题,求 的取值范围.
的取值范围.
如图,设椭圆 :
:
 的离心率
的离心率 ,顶点
,顶点 的距离为
的距离为 ,
, 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)过点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于 两点.
两点.
(ⅰ)试判断点 到直线
到直线 的距离是否为定值.若是请求出这个定值,若不是请说明理由;
的距离是否为定值.若是请求出这个定值,若不是请说明理由;
(ⅱ)求 的最小值.
的最小值.
如图,在各棱长均为 的三棱柱
的三棱柱 中,侧面
中,侧面 底面
底面 ,
, .
.
(1)求侧棱 与平面
与平面 所成的角;
所成的角;
(2)已知点 满足
满足 ,在直线
,在直线 上的点
上的点 ,满足
,满足 ,求二面角
,求二面角 的余弦值.
的余弦值.