（本小题满分12分）
有编号为l，2，3，…，
的个学生，入坐编号为1，2，3，…，的个座位．每个学生规定坐一个座位，设学生所坐的座位号与该生的编号不同的学生人数为
，已知
时，共有6种坐法．
（1）求的值；
（2）求随机变量的概率分布列和数学期望．
已知函数f(x)=
，其中
（I）若b>2a,且 f(sinx)(x∈R)的最大值为2，最小值为－4，试求函数f(x)的最小值；
（II）若对任意实数x，不等式
恒成立,且存在
成立，求c的值。
二次函数f(x)=
（I）若方程f(x)=0无实数根，求证：b>0；
（II）若方程f(x)=0有两实数根，且两实根是相邻的两个整数，求证：f(－a)=
；
（III）若方程f(x)=0有两个非整数实根，且这两实数根在相邻两整数之间，试证明存在整数k，使得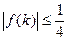
.
已知函数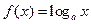
和
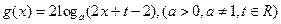的图象在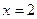
处的切线互相平行.
(Ⅰ) 求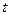
的值；
（Ⅱ）设
，当
时，
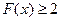恒成立，求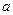
的取值范围.
斜率为2的直线l被双曲线
=1截得的弦长为4,求直线l的方程.
设双曲线与椭圆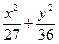
=1有共同的焦点,且与此椭圆一个交点的纵坐标为4,求这个双曲线的方程.