(本小题满分14分)
设椭圆
 (
( )的两个焦点是
)的两个焦点是 和
和 (
( ),且椭圆
),且椭圆 与圆
与圆 有公共点.
有公共点.
(1)求 的取值范围;
的取值范围;
(2)若椭圆上的点到焦点的最短距离为 ,求椭圆的方程;
,求椭圆的方程;
(3)对(2)中的椭圆 ,直线
,直线
 (
( )与
)与 交于不同的两点
交于不同的两点 、
、 ,若线段
,若线段 的垂直平分线恒过点
的垂直平分线恒过点 ,求实数
,求实数 的取值范围.
的取值范围.
为了让学生了解更多“社会法律”知识,某中学举行了一次“ 社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
1 |
0.16 |
| 70.5~80.5 |
10 |
2 |
 80.5~90.5 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
3 |
4 |
| 合计 |
50 |
1 |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格1 234并作出频率分布直方图;
234并作出频率分布直方图;
10分)(1)用辗转相除法或更相减损术求204与85的最大公约数.
(2)根据下面的要求,求满足1+2+3+…+n >500的最小的自然数n .以下是解决该问题的一个程序,但有几处错误,请找出错误并予以更正.
.以下是解决该问题的一个程序,但有几处错误,请找出错误并予以更正.
已知函数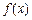 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: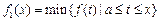
 ,
,
 .其中,
.其中,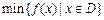 表示函数
表示函数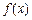 在
在 上的最小值,
上的最小值, 表示函数
表示函数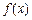 在
在 上的最大值.若存在最小正
上的最大值.若存在最小正 整数
整数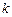 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数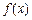 为
为 上的“
上的“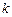 阶收缩函数”.
阶收缩函数”.
(1)已知函数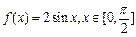 ,试写出
,试写出 ,
, 的表达式,并判断
的表达式,并判断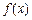 是否为
是否为 上的“
上的“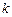 阶收缩函数”,如果是,请求对应的
阶收缩函数”,如果是,请求对应的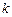 的值;如果不是,请说明理由;
的值;如果不是,请说明理由;
(2)已知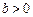 ,函数
,函数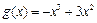 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求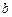 的取值范围.
的取值范围.
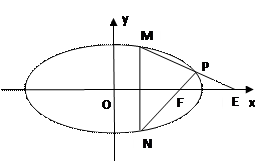
.圆锥曲线上任意两点连成的线段称为弦。若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦。已知点 、
、 是圆锥曲线C上不与顶点重合的任意两点,
是圆锥曲线C上不与顶点重合的任意两点,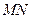 是垂直于
是垂直于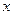 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线 分别交
分别交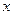 轴于点
轴于点 和点
和点 。
。
(1)试用 的代数式分别表示
的代数式分别表示
 和
和 ;
;
(2)若C的方程为 (如图),求证:
(如图),求证: 是与
是与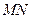 和点
和点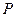 位置无关的定值;
位置无关的定值;
(3)请选定一条除椭圆外的圆锥曲线C,试探究 和
和 经过某种四则运算(加、减、乘、除),其结果是否是与
经过某种四则运算(加、减、乘、除),其结果是否是与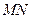 和点
和点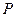 位置无关的定值,写出你的研究结论并证明。
位置无关的定值,写出你的研究结论并证明。
(说明:对于第3题,将根据研究结论所体现的思维层次,给予两种不同层次的评分)
一个房间有3扇同样的窗子,其中只有一扇窗子是打开的。有一只鸟自开着的窗子飞入这个房间,它只能从开着的窗子飞出去。鸟在房子里一次又一次地向着窗户飞去,试图飞出房间. 鸟飞向各扇窗子是随机的.
(1)假定鸟是没有记忆的,若这只鸟恰好在第x次试飞时飞出了房间,求试飞次数x的分布列;
(2)假定这只鸟是有记忆的,它飞向任一窗子的尝试不多于一次,若这只鸟恰好在第y次试飞时飞出了房间,求试飞次数y的分布列;