甲、乙两支仪仗队队员的身高(单位:cm)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180.
(1)将下表填完整:
| 身高(cm) |
176 |
177 |
178 |
179 |
180 |
| 甲队(人) |
|
3 |
4 |
|
0 |
| 乙队(人) |
2 |
1 |
|
1 |
|
(2)甲队队员身高的平均数为 cm,乙队队员身高的平均数为 cm;
(3)你认为哪支仪仗队身高更为整齐?简要说明理由.
“校园手机”现象越来越受到社会的关注﹒春节期间,小明随机调查了城区若干名同学和家长对中学生带手机现象的看法.统计整理并制作了如下的统计图:
这次的调查对象中,家长有 ▲ 人;
图②中表示家长“赞成”的圆心角的度数为 ▲ 度;
开学后,甲、乙两所学校对各自学校所有学生带手机情况进行了统计,发现两校共有384名学生带手机,且乙学校带手机的学生数是甲学校带手机学生数的,求甲、乙两校中带手机的学生数各有多少?
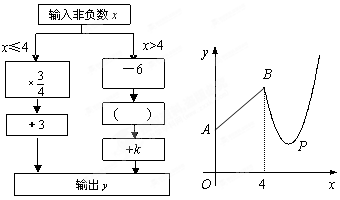
下图是数值转换机的示意图,小明按照其对应关系画出了y与x的函数图象.分别写出当0≤x≤4与x>4时,y与x的函数关系式;
小明说:“所输出y的值为3时,输入x的值为0或5.”你认为他说的对吗?试结合图象说明。
如图,梯形ABCD中, DC∥AB,点E是BC的中点,连结AE并延长与DC的延长线相交于点F,连结BF,AC.
求证:四边形ABFC是平行四边形;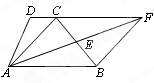
如图,已知 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为弧CF的中点,连接
为弧CF的中点,连接 交
交 于点
于点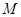 ,
, 为△ABC的角平分线,且
为△ABC的角平分线,且 ,垂足为点
,垂足为点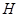 .
.求证:
 是半圆
是半圆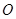 的切线;
的切线;若
 ,
, ,求
,求 的长.
的长.
当太阳光线与地面成45o角时,在坡度为i="1:2" 的斜坡上的一棵树AB落在坡面上的影子AC长为5米,落在水平线上的影子CD长为3米,求这棵树的高度(参考数据 ,
, ,
, ,结果保留两个有效数字).
,结果保留两个有效数字).