在平面直角坐标系xOy中,直线 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.
(1)求∠BAO的度数;
(2)如图1,P为线段AB上一点,在AP上方以AP为斜边作等腰直角三角形APD.点Q在AD上,连结PQ,过作射线PF⊥PQ交x轴于点F,作PG⊥x轴于点G.
求证:PF=PQ ;
(3)如图2,E为线段AB上一点,在AE上方以AE为斜边作等腰直角三角形AED.若P为线段EB的中点,连接PD、PO,猜想线段PD、PO有怎样的关系?并说明理由.
计算

已知抛物线的顶点是 (
( ,
,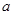 为常数),并经过点
为常数),并经过点 点
点 为一定点.
为一定点.
求含有常数
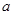 的抛物线的解析式;
的抛物线的解析式;设点P是抛物线上任意一点,过P作PH⊥
 轴,垂足是H,求证:PD=PH;
轴,垂足是H,求证:PD=PH;设过原点O的直线与抛物线在第一象限相交A、B两点,若DA=2DB,且
 ,求
,求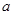 的值
的值
如图,已知线段AB∥CD,AD与B C相交于点K,E是线段AD上一动点.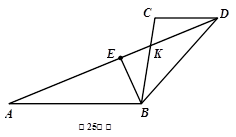
若BK=
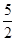 KC,求
KC,求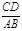 的值
的值连接BE,若BE平分∠ABC,则当AE=
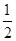 AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明再探究:当AE=
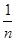 AD(
AD(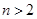 ),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
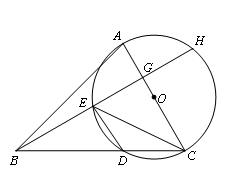
如图,在△ABC中,以AC边为直径的⊙O交BC边于点D,在劣弧上取一点E,并使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H求证:AC⊥BH
若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长
为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.