本题满分分 已知函数f (x)=x3+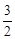 (1-a)x2-3ax+1,a>0.
(1-a)x2-3ax+1,a>0.
(Ⅰ) 证明:对于正数a,存在正数p,使得当x∈[0,p]时,有-1≤f (x)≤1;
(Ⅱ) 设(Ⅰ)中的p的最大值为g(a),求g(a)的最大值.
斜率为2的直线 经过抛物线
经过抛物线 的焦点
的焦点 ,且与抛物线相交于
,且与抛物线相交于 两点,求线段
两点,求线段 的长.
的长.
已知 :“直线
:“直线 与圆
与圆 相交”;
相交”; :“方程
:“方程 的两根异号”.若
的两根异号”.若 为真,
为真, 为真,求实数
为真,求实数 的取值范围.
的取值范围.
已知椭圆E的长轴长与焦距比为2:1,左焦点F(﹣2,0),一定点为P(﹣8,0).
(1)求椭圆E的标准方程;
(2)过P的直线与椭圆交于P1、P2两点,设直线P1F、P2F的斜率分别为k1、k2,求证:k1+k2=0.
(3)求△P1P2F面积的最大值.
已知二次函数f(x)=x2+x的定义域为D恰是不等式 的解集,其值域为A,函数g(x)=x3﹣3tx+
的解集,其值域为A,函数g(x)=x3﹣3tx+ 的定义域为[0,1],值域为B.
的定义域为[0,1],值域为B.
(1)求函数f(x)定义域为D和值域A;
(2)是否存在负实数t,使得A⊆B成立?若存在,求负实数t的取值范围;若不存在,请说明理由;
(3)若函数g(x)=x3﹣3tx+ 在定义域[0,1]上单调递减,求实数t的取值范围.
在定义域[0,1]上单调递减,求实数t的取值范围.
已知 =(cos2
=(cos2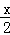 ,
,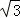 sinx),
sinx),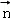 =(2,1),设函数f(x)=
=(2,1),设函数f(x)=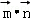 .
.
(1)当x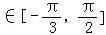 ,求函数f(x)的值域;
,求函数f(x)的值域;
(2)当f(α)= ,且﹣
,且﹣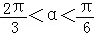 ,求sin(2
,求sin(2 )的值.
)的值.