(本小题满分12分)
已知椭圆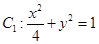 ,椭圆
,椭圆 以
以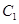 的长轴为短轴,且与
的长轴为短轴,且与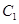 有相同的离心率.
有相同的离心率.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆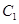 和
和 上,
上,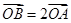 ,求直线
,求直线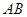 的方程.
的方程.
(本小题满分14分)
设椭圆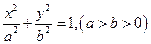 的左右焦点分别为
的左右焦点分别为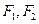 ,离心率
,离心率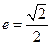 ,点
,点 在直线
在直线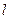 :
: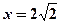 的左侧,且F2到l的距离为
的左侧,且F2到l的距离为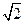 。
。
(1)求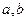 的值;
的值;
(2)设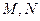 是
是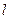 上的两个动点,
上的两个动点,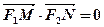 ,证明:当
,证明:当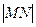 取最小值时,
取最小值时,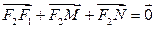
(本小题满分14分)
已知正数数列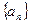 满足:
满足: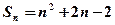 ,其中
,其中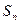 为数列
为数列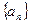 的前
的前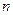 项和.
项和.
(1)求数列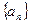 的通项
的通项 ;
;
(2)令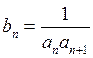 ,求
,求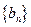 的前n项和Tn.
的前n项和Tn.
(本小题满分12分)

已知点M的坐标为(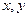 ),且
),且 。
。
(1)当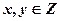 时,求点M在区域
时,求点M在区域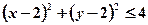 内的概率;
内的概率;
(2)当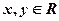 时,求点M在区域
时,求点M在区域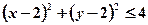 内的概率。
内的概率。
(本小题满分12分)
已知函数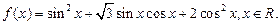
(1)求函数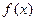 的最小正周期;
的最小正周期;
(2)当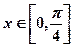 时,求函数f (x) 的最大值与最小值及相应的
时,求函数f (x) 的最大值与最小值及相应的 值。
值。
某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水
化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳
水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中
至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,
并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?