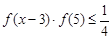在平面直角坐标系中, 的两个顶点
的两个顶点 、
、 的坐标分别是(-1,0),(1,0),点
的坐标分别是(-1,0),(1,0),点 是
是 的重心,
的重心,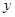 轴上一点
轴上一点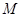 满足
满足 ,且
,且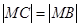 .
.
(1)求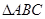 的顶点
的顶点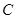 的轨迹
的轨迹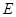 的方程;
的方程;
(2)不过点 的直线
的直线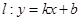 与轨迹
与轨迹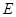 交于不同的两点
交于不同的两点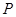 、
、 ,当
,当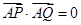 时,求
时,求 与
与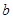 的关系,并证明直线
的关系,并证明直线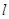 过定点.
过定点.
已知数列 的前
的前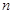 项和为
项和为 ,
, ,且
,且 (
(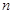 为正整数)
为正整数)
(Ⅰ)求出数列 的通项公式;
的通项公式;
(Ⅱ)若对任意正整数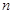 ,
, 恒成立,求实数
恒成立,求实数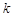 的最大值.
的最大值.
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。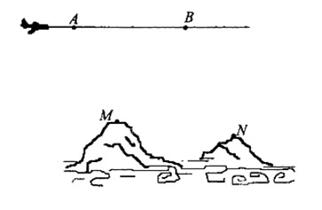
设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的格点(格点即横坐标和纵坐标均为整数的点)的个数为
内的格点(格点即横坐标和纵坐标均为整数的点)的个数为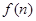 (
( ).
).
(Ⅰ)求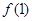 、
、 的值及
的值及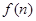 的表达式;
的表达式;
(Ⅱ)设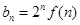 ,
, 为
为 的前
的前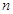 项和,求
项和,求 .
.
已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,其值为正,而当x∈(-∞,-2)∪(6,+∞)时,其值为负.
(Ⅰ)求实数a,b的值及函数f(x)的表达式;
(Ⅱ)设F(x)=- f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
.若非零函数 对任意实数
对任意实数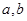 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当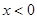 时,
时, .
.
(1)求证: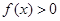 ;
;
(2)求证: 为减函数;
为减函数;
(3)当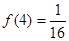 时,解不等式
时,解不等式