已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,其值为正,而当x∈(-∞,-2)∪(6,+∞)时,其值为负.
(Ⅰ)求实数a,b的值及函数f(x)的表达式;
(Ⅱ)设F(x)=- f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
(本小题满分12分)甲、乙两家药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
(1)求a;
(2)某医院计划采购一批该型号药品,从质量的稳定性角度考虑,你认为采购哪个药厂的产品比较合适?
(3)检测单位从甲厂送检的样品中任取两份作进一步分析,在抽取的两份样品中,求至少有一份得分在(90,100]之间的概率.
(本小题满分12分)已知锐角△ABC中的三个内角分别为A,B,C.
(1)设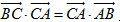 ,求证△ABC是等腰三角形;
,求证△ABC是等腰三角形;
(2)设向量s=(2sinC,- ),t=(cos2C,2
),t=(cos2C,2 -1),且s∥t,若sinA=
-1),且s∥t,若sinA= ,求sin(
,求sin( -B)的值.
-B)的值.
(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,C= ,a=5,△ABC的面积为10
,a=5,△ABC的面积为10 .
.
(1)求b,c的值;
(2)求cos(B- )的值.
)的值.
(本小题满分14分)设函数f(x)=x2+aln(x+1).
(1)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(2)若函数y=f(x)有两个极值点x1,x2,且x1<x2,求证: .
.
(本小题满分13分)设F1,F2分别是椭圆 的左右焦点.
的左右焦点.
(1)若P是该椭圆上的一个动点,求 的最大值和最小值.
的最大值和最小值.
(2)是否存在经过点A(5,0)的直线l与椭圆交于不同的两点C,D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.