某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
(本小题满分14分)设函数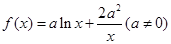 .
.
(Ⅰ)已知曲线 在点
在点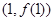 处的切线
处的切线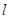 的斜率为
的斜率为 ,求实数
,求实数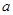 的值;
的值;
(Ⅱ)讨论函数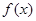 的单调性;
的单调性;
(Ⅲ)在(Ⅰ)的条件下,求证:对于定义域内的任意一个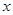 ,都有
,都有 .
.
(本小题满分13分)
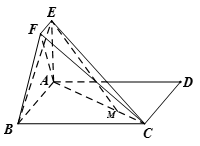
如图,四边形 为正方形,
为正方形, 平面
平面 ,
, ,
, .
.
(Ⅰ)求证: 
(Ⅱ)若点 在线段
在线段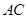 上,且满足
上,且满足 ,求证:
,求证: 平面
平面 ;
;
(Ⅲ)试判断直线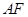 与平面
与平面 是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
(本小题满分13分)
高三年级进行模拟考试,某班参加考试的40名同学的成绩统计如下:
| 分数段 |
(70,90) |
[90,100) |
[100,120) |
[120,150] |
| 人数 |
5 |
a |
15 |
b |
规定分数在90分及以上为及格,120分及以上为优秀,成绩高于85分低于90分的同学为希望生.已知该班希望生有2名.
(Ⅰ)从该班所有学生中任选一名,求其成绩及格的概率;
(Ⅱ)当a =11时,从该班所有学生中任选一名,求其成绩优秀的概率;
(Ⅲ)从分数在(70,90)的5名学生中,任选2名同学参加辅导,求其中恰有1名希望生的概率.
(本小题满分13分)
已知函数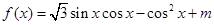
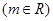 的图象过点
的图象过点 .
.
(Ⅰ)求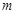 的值;
的值;
(Ⅱ)在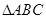 中,角
中,角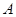 ,
, ,
,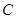 的对边分别是
的对边分别是 ,
,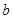 ,
,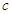 ,若
,若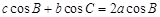 求
求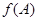 的取值范围.
的取值范围.
数列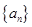 是等差数列,
是等差数列,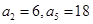 ;数列
;数列 的前n项和是
的前n项和是 ,且
,且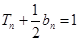 .
.
(1) 求数列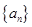 的通项公式; (2) 求证:数列
的通项公式; (2) 求证:数列 是等比数列;
是等比数列;
(3) 记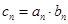 ,求
,求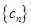 的前n项和
的前n项和