(本小题满分12分)
在平面直角坐标系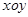 中,点
中,点 到两定点F1
到两定点F1 和F2
和F2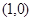 的距离之和为
的距离之和为 ,设点
,设点 的轨迹是曲线
的轨迹是曲线 .(1)求曲线
.(1)求曲线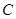 的方程; (2)若直线
的方程; (2)若直线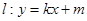 与曲线
与曲线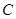 相交于不同两点
相交于不同两点 、
、 (
( 、
、 不是曲线
不是曲线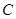 和坐标轴的交点),以
和坐标轴的交点),以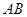 为直径的圆过点
为直径的圆过点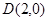 ,试判断直线
,试判断直线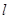 是否经过一定点,若是,求出定点坐标;若不是,说明理由.
是否经过一定点,若是,求出定点坐标;若不是,说明理由.
已知函数 ,数列
,数列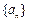 满足
满足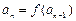 (n≥2,nÎN*).
(n≥2,nÎN*).
若 ,数列
,数列 满足
满足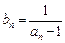
(1)求证:数列 是等差数列;
是等差数列;
(2)设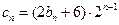 ,求数列
,求数列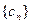 的前n项和
的前n项和 。
。
某公司一年需要一种计算机元件8000个,每天需同样多的元件用于组装整机,该元件每年分 次进货,每次购买元件的数量均为
次进货,每次购买元件的数量均为 ,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为
,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为 件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
双曲线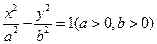 的离心率
的离心率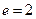 ,
, 是左,右焦点,过
是左,右焦点,过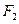 作
作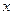 轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知
轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知
(1)求双曲线的方程;
(2)设过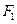 的直线MN分别与左支,右支交于M、N ,线段MN的垂线平分线
的直线MN分别与左支,右支交于M、N ,线段MN的垂线平分线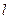 与
与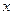 轴交于点
轴交于点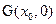 ,若
,若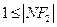 <3,求
<3,求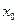 的取值范围。
的取值范围。
已知函数
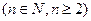
(1)当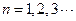 时,把已知函数的图像与直线
时,把已知函数的图像与直线 的交点的横坐标依次为
的交点的横坐标依次为 求证:
求证: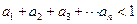
(2)对于每一个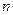 的值,设
的值,设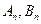 为已知函数的图上与
为已知函数的图上与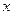 轴距离为1的两点,求证:
轴距离为1的两点,求证: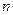 取任意一个正数时,以
取任意一个正数时,以 为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
已知函数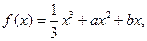 且
且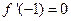
(1)求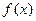 的单调区间;
的单调区间;

(2)令 ,设函数
,设函数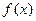 在
在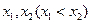 处取得极值
处取得极值 ,记点
,记点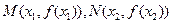 ,证明:线段
,证明:线段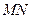 与曲线
与曲线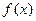 存在异于
存在异于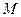 、
、
 的公共点;
的公共点;