(本小题满分12分)
已知函数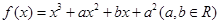
(1)若函数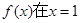 处有极值10,求b的值;
处有极值10,求b的值;
(2)若对任意 上单调递增,求b的取值范围。
上单调递增,求b的取值范围。
某体育彩票规定:从01到36共36个号中抽出7个号为一注,每注2元.某人想先选定吉利号18,然后从01至17中选3个连续的号,从19至29中选2个连续的号,从30至36中选1个号组成一注.若这个人要把这种要求的号全买下,至少要花多少元钱?
已知集合M={-3,-2,-1,0,1,2},P(a,b)表示平面上的点(a,b∈M),问:
(1)P可表示平面上多少个不同的点?
(2)P可表示平面上多少个第二象限的点?
(3)P可表示多少个不在直线y=x上的点?
在所有的两位数中,个位数字大于十位数字的两位数共有多少个?
某工厂2008年的生产总值100万元,技术革新后预计以后每年的生产总值比上一年增加5%,问最早需要哪一年年生产总值超过200万元.写出计算的一个算法并画出相应的程序框图.
已知 ,将区间
,将区间 10等分,画出求各等分点及端点函数值的程序框图.
10等分,画出求各等分点及端点函数值的程序框图.