(10分)某班40名学生的某次数学测验的平均成绩是69分,成绩统计表如下:
| 成绩 |
50 |
60 |
70 |
80 |
90 |
100 |
| 人数(人) |
2 |
x |
10 |
y |
4 |
2 |
(1)求x和y的值;
(2)设此班40名学生成绩的众数为 ,中位数为
,中位数为 ,求代数式
,求代数式 的值。
的值。
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD=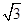 ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.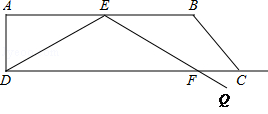
(1)求下底DC的长度;
(2)当点E是AB的中点时,求线段DF的长度;
(3)请计算射线EF经过点C时,AE的长度.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 (k≠0)在第一象限内的图象经过点D、E,且tan ∠ BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan ∠ BOA=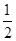 .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
庆华中学为丰富学生的校园生活,准备从某体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元.购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据庆华中学的实际情况,需从该体育用品商店一次性购买足球和篮球共100个.要求购买足球和篮球的总费用不超过6000元,这所中学最多可以购买多少个篮球?
某中学组织全校4 000名学生进行了民族团结知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图6的频数分布表和频数分布直方图(不完整).

请根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)上述学生成绩的中位数落在哪一组范围内?
(4)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校4 000名学生中约有多少名获奖?
(1)如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF⊥AG于点F.
求证:AE=BF
(2)如图,□ABCD中,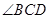 的平分线
的平分线 交边
交边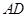 于
于 ,
, 的平分线
的平分线 交
交 于
于 ,交
,交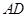 于
于 .若AB=3,BC=5,求EG的长。
.若AB=3,BC=5,求EG的长。