以坐标原点为极点，横轴的正半轴为极轴的极坐标系下，有曲线C：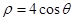
，过极点的直线
（
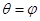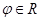且
是参数）交曲线C于两点0，A，令OA的中点为M.
(1)求点M在此极坐标下的轨迹方程（极坐标形式）.
(2)当
时，求M点的直角坐标.
已知等比数列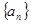
中，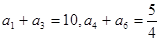
，求其第4项及前5项和.
已知直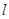线
经过抛物线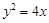
的焦点F，且与抛物线相交于A、B两点.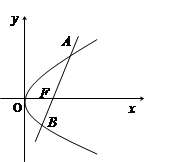
（1）若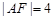
，求点A的坐标；
（2）若直线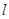的倾斜角为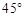
，求线段AB的长.
在正三棱柱ABC-A1B1C1中，若BB1=1，AB=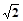
，求AB1与C1B所成角的大小。
已知椭圆的两焦点是F1(0，-1)，F2(0,1)，离心率e=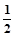
(1)求椭圆方程；(2)若P在椭圆上，且|PF1|-|PF2|=1，求cos∠F1PF2。
已知函数f（x）＝（1＋x）2－4a lnx（a∈N﹡）．
（Ⅰ）若函数f（x）在（1，＋∞）上是增函数，求a的值；
（Ⅱ）在（Ⅰ）的条件下，若关于x的方程f（x）＝x2－x＋b在区间[1，e]上恰有一个实根，求实数b的取值范围．