如图所示，水平固定放置的平行金属板M、N，两板间的距离为d，在两板的中心（即到上、下板距离相等，到板左、右端距离相等）有一悬点O，系有一长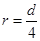
的绝缘细线，线的另一端系有一质量为m、带正电荷的小球，电荷量为q。现对两板充电，使得两板间形成一竖直向上的匀强电场，匀强电场的大小为
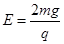。求：
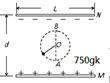
（1）小球静止时，细线的拉力大小
（2）现给小球以速度，要使得小球在竖直平面内绕O点做完整的圆周运动，小球在整个圆周运动中的最小速度多大？
（3）小球能绕悬点O在竖直平面内做完整的圆周运动，当小球运动到竖直直径AB的B端时，细线突然断开，设此时其水平速度大小为
，小球恰好从平行金属板的边界飞出，求平行金属板的长度L。
某野战部队科研小组采用了偏二甲肼加氧化二氮(氧化剂)为燃料，精心研制了一枚小型火箭，现点燃火箭使火箭在垂直于地面的方向上运动.火箭点火后可认为做匀加速直线运动，经过5 s 到达离地面100 m高处时燃料恰好用完，若不计空气阻力，取g=" 10" m/s2，求:燃料恰好用完时火箭的速度.
火箭上升离地面的最大高度.
火箭从发射到残骸落回地面所用的总时间.
如图所示，在xoy坐标平面的第一象限内有沿－y方向的匀强电场，在第四象限内有垂直于平面向外的匀强磁场。现有一质量为m，带电量为-q的粒子（重力不计）以初速度v0沿－x方向从坐标为（3L、L）的P点开始运动，接着进入磁场，最后由坐标原点射出，射出时速度方向与y轴方间夹角为45º，求：粒子从O点射出时的速度v和电场强度E；
粒子从P点运动到O点过程所用的时间。
如图所示，固定的光滑圆弧轨道
的半径为0.8m，
点与圆心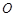
在同一水平线上，圆弧轨道底端
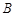点与圆心在同一竖直线上. 
点离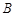点的竖直高度为0.2m.物块从轨道上的点由静止释放，滑过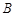点后进入足够长的水平传送带，传送带由电动机驱动按图示方向运转，不计物块通过轨道与传送带交接处的动能损失，物块与传送带间的动摩擦因数为0.1，
取10m/s2.
求物块从
点下滑到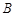点时速度的大小.若物块从
点下滑到传送带上后，又恰能返回到点，求物块在传送带上第一次往返所用的时间.
航模兴趣小组设计出一架遥控飞机，其质量m=2kg，动力系统提供的恒定升力F=28N。试飞时，飞机从地面由静止开始竖直上升。设飞机飞行时所受的阻力大小不变，g=10m/s
则第一次试飞，飞机飞行t
=8s时到达的高度H=64m。求飞机所受阻力的f的大小。第二次试飞，飞机飞行t
=6s时遥控器出现故障，飞机立即失去升力。求飞机能到达的最大高度h。
近地人造卫星1和2绕地球做匀速圆周运动的周期分别为
和
,设在卫星1、卫星2各自所在的高度上的重力加速度大小分别为
、
，求
的比值。