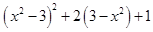 分解因式.
分解因式.
(1)关于x的方程2x一3=2m+8的解是负数,求m的取值范围.
(2)如果代数式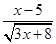 有意义,求x的取值范围.
有意义,求x的取值范围.
如图,甲轮船以16海里/时的速度离开港口O,向东南方向航行,乙轮船在同时同地,向西南方向航行.已知:它们离开港口O一个半小时后,相距30海里,求:乙轮船每小时航行多少海里? 
若∠C=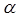 ,∠EAC+∠FBC=
,∠EAC+∠FBC=
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则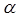 与
与 有何关系?并说明理由.
有何关系?并说明理由.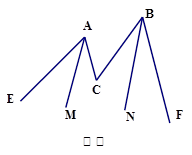
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与 、
、 的关系是 .(用
的关系是 .(用 、
、 表示)
表示)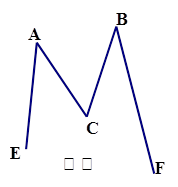
(3)如图③,若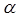 ≥
≥ ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于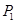 ,
, 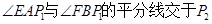 ;依此类推,则
;依此类推,则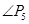 = (用
= (用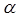 、
、 表示)
表示)
探究发现:阅读解答题:在数学中,有些大数值问题可以通过用字母代替数转化成整式问题来解决.例:试比较20142015×20142012与20142014×20142013的大小.
解:设20142014=a,x=20142015×20142012,
y= 20142014×20142013
那么x=(a+1)(a-2),
那么y= a(a-1)
∵x-y=
∴
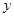 (填>、<).
(填>、<).
填完后,你学到了这种方法吗?不妨尝试一下,相信你准行!
问题:计算.(m+22.2014)(m+14.2014)-(m+18.2014)(m+17.2014)