(本小题满分12分)已知向量 =3i-4j,
=3i-4j, =6i-3j,
=6i-3j, =(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
=(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
(1)A,B,C能够成三角形,求实数m应满足的条件。
(2)对任意m∈[1,2]使不等式 2≤-x2+x+3恒成立,求x的取值范围
2≤-x2+x+3恒成立,求x的取值范围
如图,椭圆C0: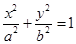 (a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.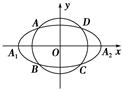
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2=t22与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:t12+t22为定值.
已知函数f(x)=x3+ax2+bx.
(1)若函数y=f(x)在x=2处有极值-6,求y=f(x)的单调递减区间;
(2)若y=f(x)的导数f′(x)对x∈[-1,1]都有f′(x)≤2,求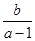 的取值范围.
的取值范围.
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
已知数列{an}是等差数列,{bn}是等比数列,且a1=b1=2,b4=54,a1+a2+a3=b2+b3.
(1)求数列{an}和{bn}的通项公式;
(2)数列{cn}满足cn=anbn,求数列{cn}的前n项和Sn.
如图,已知四棱锥P—ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点.
(1)证明:PE⊥BC;
(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.