(本小题共8分)
已知函数f(x)对任意实数x,y都有f(x+y)=f(x)+f(y),且当x>0时,f(x)>0,f(-1)=-2,求f(x)在[-2,1]上的值域。
(本小题满分8分)已知函数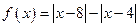 .
.
(Ⅰ)作出函数 的图象;
的图象;
(Ⅱ)解不等式
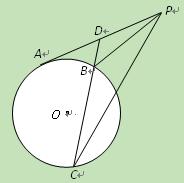
(本小题满分8分)如图, 切⊙O于点
切⊙O于点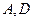 为
为 的中点,过点
的中点,过点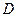 引割线交⊙O于
引割线交⊙O于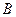 、
、 两点.求证:
两点.求证: .
.
(本小题满分8分)直线 过点
过点 ,且倾斜角为
,且倾斜角为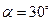 .
.
(I)求直线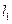 的参数方程;
的参数方程;
(II)若直线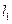 和直线
和直线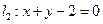 交于点
交于点 ,求
,求 .
.
(本小题满分10分)甲、乙两人进行一次象棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束.假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局.
(Ⅰ)求甲获得这次比赛胜利的概率;
(Ⅱ)设ξ表示从第3局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.
(本小题满分10分)设函数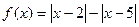 ,
,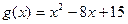 。
。
(1)证明: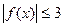 ;
;
(2)求不等式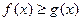 的解集;
的解集;
(3)当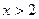 时,求函数
时,求函数 的最大值。
的最大值。