已知函数 ,设曲线
,设曲线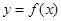 在与
在与 轴交点处的切线为
轴交点处的切线为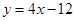 ,
,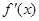 为
为 的导函数,满足
的导函数,满足 .
.
(1)求 的单调区间.
的单调区间.
(2)设 ,
,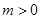 ,求函数
,求函数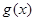 在
在 上的最大值;
上的最大值;
∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°∠BDC=15°(如图)求:炮兵阵地到目标的距离.
| 资金 |
每台空调或冰箱所需资金(百元) |
月资金供应数量 (百元) |
|
| 空调 |
冰箱 |
||
| 成本 |
30 |
20 |
300 |
| 工人工资 |
5 |
10 |
110 |
| 每台利润 |
6 |
8 |
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?最大利润是多少?
在等差数列{an}中,a1+a3=8,且a4为a2和a9的等比中项,求数列{an}的首项,公差及前n项和.
(2)是否存在m使得不等式2x-1>m(x2-1)对满足|x|≤2的一切实数x的取值都成立.
为了了解参加某种知识竞赛的1003名学生的成绩,请用系统抽样抽取一个容量为50的样本.