函数 的图象与函数
的图象与函数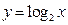 的图象交于两点
的图象交于两点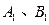 (
(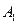 在线段
在线段 上,
上, 为坐标原点),过
为坐标原点),过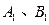 作
作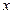 轴的垂线,垂足分别为
轴的垂线,垂足分别为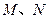 ,并且
,并且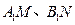 分别交函数
分别交函数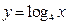 的图象于
的图象于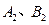 两点.
两点.
(1)试探究线段 的大小关系;
的大小关系;
(2)若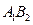 平行于
平行于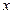 轴,求四边形
轴,求四边形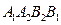 的面积.
的面积.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是地面边长的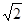 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P-AC-D的大小
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。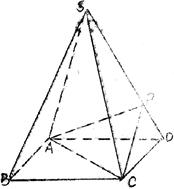
.如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=40°
(1)求证:EF⊥平面BCE;
(2)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE
(3)求二面角F—BD—A的大小。
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=A,AB=2,以AC的中点O为球心、AC为直径的球面交PD于点M。
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成的角的大小;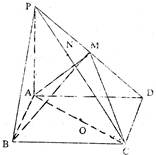
已知△ABC的面积S满足
(Ⅰ)求θ的取值范围;
(Ⅱ)求函数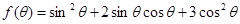 的最大值。
的最大值。
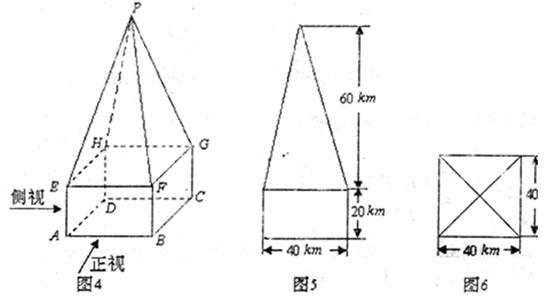
.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P—EFGH,下半部分是长方体ABCD—EFGH,图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线BD⊥平面PEG