(本小题满分12分)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段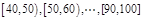 ,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题: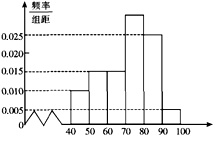
(1)求70~80分数段的学生人数;
(2)估计这次考试中该学科的优分率(80分及以上为优分)、中位数、平均值;
(3)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
已知抛物线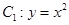 ,
,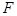 为抛物线的焦点,椭圆
为抛物线的焦点,椭圆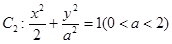 ;
;
(1)若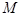 是
是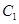 与
与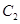 在第一象限的交点,且
在第一象限的交点,且 ,求实数
,求实数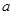 的值;
的值;
(2)设直线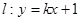 与抛物线
与抛物线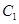 交于
交于 两个不同的点,
两个不同的点, 与椭圆
与椭圆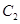 交于
交于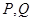 两个
两个
不同点,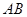 中点为
中点为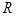 ,
, 中点为
中点为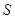 ,若
,若 在以
在以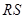 为直径的圆上,且
为直径的圆上,且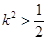 ,求实数
,求实数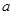
的取值范围.
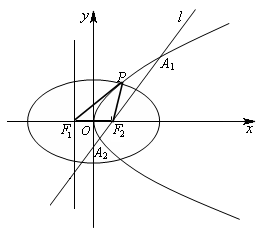
如图,设抛物线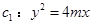 (
(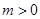 )的准线与
)的准线与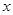 轴交于
轴交于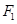 ,焦点为
,焦点为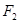 ;以
;以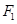 、
、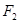 为焦点,离心率
为焦点,离心率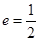 的椭圆
的椭圆 与抛物线
与抛物线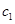 在
在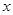 轴上方的一个交点为
轴上方的一个交点为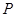 .
.
(1)当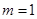 时,求椭圆的方程;
时,求椭圆的方程;
(2)在(1)的条件下,直线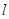 经过椭圆
经过椭圆 的右焦点
的右焦点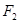 ,与抛物线
,与抛物线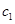 交于
交于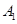 、
、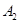 ,如果以线段
,如果以线段 为直径作圆,试判断点
为直径作圆,试判断点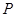 与圆的位置关系,并说明理由;
与圆的位置关系,并说明理由;
(3)是否存在实数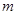 ,使得
,使得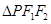 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数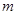 ;若不存在,请说明理由.
;若不存在,请说明理由.
已知函数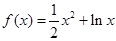 .
.
(1)求函数 在区间
在区间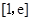 上的最大、最小值;
上的最大、最小值;
(2)求证:在区间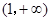 上,函数
上,函数 的图象在函数
的图象在函数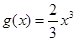 的图象的下方.
的图象的下方.
(1)已知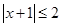 ,
, ,求证:
,求证: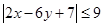 ;
;
(2)已知正数 满足关系
满足关系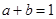 ,求证:
,求证: .
.
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 |
A样式 |
B样式 |
C样式 |
| 10W |
2000 |
z |
3000 |
| 30W |
3000 |
4500 |
5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.