(本小题满分13分)
已知 ,
, 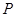 是平面上一动点,
是平面上一动点, 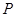 到直线
到直线 上的射影为点
上的射影为点 ,且满足
,且满足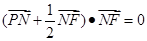
(Ⅰ)求点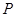 的轨迹
的轨迹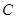 的方程;
的方程;
(Ⅱ)过点 作曲线
作曲线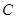 的两条弦
的两条弦 , 设
, 设 所在直线的斜率分别为
所在直线的斜率分别为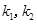 , 当
, 当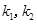 变化且满足
变化且满足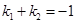 时,证明直线
时,证明直线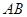 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.
(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|x+1|+|x﹣2|﹣m
(I)当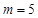 时,求f(x) >0的解集;
时,求f(x) >0的解集;
(II)若关于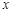 的不等式f(x) ≥2的解集是
的不等式f(x) ≥2的解集是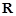 ,求
,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线C1: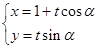 (t为参数),圆C2:
(t为参数),圆C2: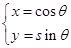 (θ为参数).
(θ为参数).
(I)当α=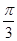 时,求C1与C2的交点的直角坐标;
时,求C1与C2的交点的直角坐标;
(II)过坐标原点O作 C1的垂线,垂足为A,P为OA的中点.当α变化时,求P点轨迹的参数方程,并指出它是什么曲线.
C1的垂线,垂足为A,P为OA的中点.当α变化时,求P点轨迹的参数方程,并指出它是什么曲线.
.选修 4-1:几何证明选讲
4-1:几何证明选讲
如图,直线 经过⊙
经过⊙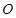 上的点
上的点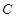 ,并且
,并且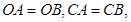 ⊙
⊙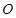 交直
交直 线
线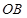 于
于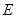 ,
,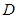 ,连接
,连接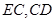 .
.
(I)求证:直线 是⊙
是⊙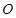 的切线;
的切线;
(II)若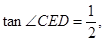 ⊙
⊙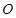 的半径为
的半径为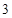 ,求
,求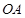 的长.
的长.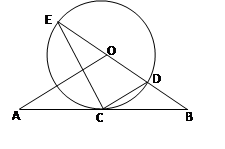
(本小题满分12分)
已知函数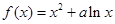
(Ⅰ)当a=﹣2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)=  +
+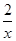 在
在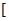 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.
(本小题满分12分)
已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为 和
和 ,且|
,且|
 |=2,
|=2,
点(1, )在该椭圆上.
)在该椭圆上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过 的直线
的直线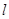 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A B的面积为
B的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线
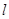 相切是圆的方程.
相切是圆的方程.