一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4,
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率。
(本小题满分12分)已知函数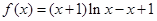
(1)若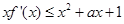 ,求
,求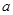 的取值范围
的取值范围
(2)证明: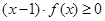
(本小题满分12分)设 ,且曲线
,且曲线 在
在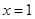 处的切线与
处的切线与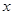 轴平行
轴平行
(1)求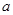 的值,并讨论
的值,并讨论 的单调性;
的单调性;
(2)证明:当 时,
时,
(本小题满分12分)某商场销售某种商品的经验表明,该商品每日的销售量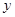 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中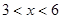 ,
,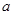 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求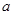 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大
的值,使商场每日销售该商品所获得的利润最大
(本小题满分12分)已知等差数列 满足:
满足: ,
,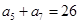 ,
, 的前
的前 项和为
项和为 .
.
(1)求 及
及 ;
;
(2)令

 ,求数列
,求数列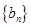 的前n项和
的前n项和 .
.
(本小题满分12分)已知向量
(1)当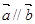 时,求
时,求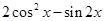 的值;
的值;
(2)求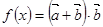 在
在 上的值域.
上的值域.