已知数列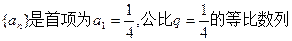
，设
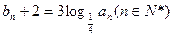，数列
。
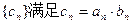（1）求证：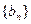
是等差数列；
（2）求数列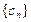
的前n项和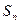
；
(本题满分10分) 
已知函数
（
）在一个周期内的图象如右图，
(Ⅰ) 求函数的解析式。
(Ⅱ)求函数的单调递增区间。
若平面内给定三个向量
，
（1）求
。
（2）求满足
的实数m，n的值。
椭圆G：
的两个焦点为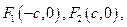
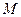是椭圆上一点，且满
．
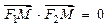（１）求离心率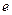
的取值
范围；
（２）当离心率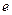取得最小值时，点
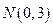到椭圆上点的最远距离为
．
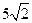①求此时椭圆G的方程；
②设斜率为
的直线
与椭圆G相交于不同两点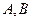
，
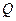为
的中点，问：
已知圆C：
，直线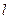
：
.
（1）当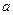
为何值时，直线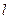与圆C相切；
（2）当直线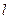与圆C相交于A、B两点，且
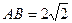时，求
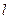直线的方程.
已知椭圆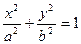
(a＞b＞0)的离心率
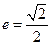, 直线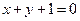
与椭圆交于P,Q两点, 且OP⊥OQ(如图) ．
（1）求证：
；
（2）求这个椭圆方程．