设函数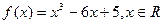 .
.
(1)求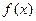 的单调区间和极值;
的单调区间和极值;
(2)若关于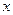 的方程
的方程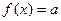 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.
(3)已知当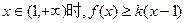 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
设二次函数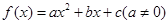 满足条件:(1)当
满足条件:(1)当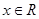 时,都有
时,都有 且
且 成立;(2)当
成立;(2)当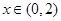 时,
时,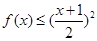 ;(3)
;(3)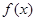 在
在 上的最小值为0.
上的最小值为0.
(1)求 的值及
的值及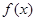 的解析式;
的解析式;
(2)求最大的实数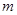 ,使得存在
,使得存在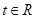 ,只要
,只要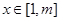 ,就有
,就有 成立.
成立.
定义在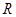 上的函数
上的函数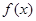 满足:
满足: 对任意
对任意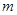 、
、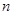
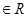 恒成立,当
恒成立,当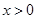 时,
时,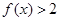 .
.
(1)求证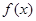 在
在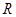 上是单调递增函数;
上是单调递增函数;
(2)已知 ,解关于
,解关于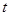 的不等式
的不等式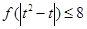 ;
;
(3)若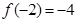 ,且不等式
,且不等式 对任意
对任意 恒成立.求实数
恒成立.求实数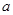 的取值范围.
的取值范围.
设函数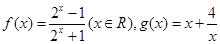
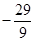
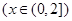
(1)求证: 是奇函数,
是奇函数,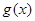 在区间
在区间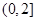 上是单调递减函数;
上是单调递减函数;
(2)若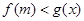 对任意
对任意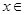
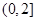 恒成立,求实数
恒成立,求实数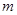 的取值范围.
的取值范围.
已知关于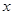 的不等式
的不等式
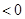 的解集是
的解集是 ,函数
,函数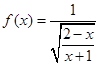 的定义域是
的定义域是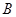 ,若
,若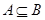 .求实数
.求实数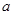 的取值范围.
的取值范围.
已知二次函数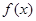 满足:(1)
满足:(1)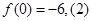 关于
关于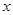 的方程
的方程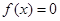 的两实根是
的两实根是 .
.
(1)求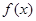 的解析式;
的解析式;
(2)设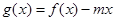 ,且
,且 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数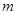 的取值范围.
的取值范围.