设二次函数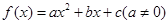 满足条件:(1)当
满足条件:(1)当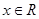 时,都有
时,都有 且
且 成立;(2)当
成立;(2)当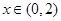 时,
时,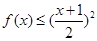 ;(3)
;(3)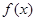 在
在 上的最小值为0.
上的最小值为0.
(1)求 的值及
的值及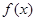 的解析式;
的解析式;
(2)求最大的实数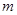 ,使得存在
,使得存在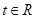 ,只要
,只要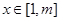 ,就有
,就有 成立.
成立.
(本小题满分14分)已知函数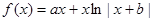 是奇函数,且图像在点
是奇函数,且图像在点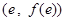 处的切线斜率为3(
处的切线斜率为3(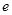 为自然对数的底数).
为自然对数的底数).
(1)求实数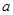 、
、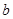 的值;
的值;
(2)若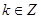 ,且
,且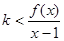 对任意
对任意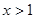 恒成立,求
恒成立,求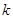 的最大值.
的最大值.
(本小题满分14分)如图,已知椭圆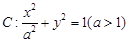 的上顶点为
的上顶点为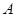 ,离心率为
,离心率为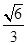 ,若不过点
,若不过点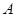 的动直线
的动直线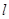 与椭圆
与椭圆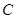 相交于
相交于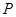 、
、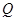 两点,且
两点,且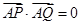 .
.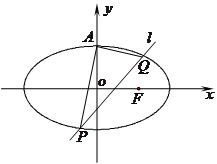
(1)求椭圆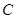 的方程;
的方程;
(2)求证:直线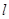 过定点,并求出该定点
过定点,并求出该定点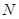 的坐标.
的坐标.
(本小题满分14分)已知 、
、 是方程
是方程 的两根,数列
的两根,数列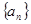 是递增的等差数列,数列
是递增的等差数列,数列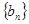 的前
的前 项和为
项和为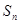 ,且
,且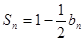 (
( ).
).
(1)求数列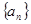 ,
,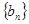 的通项公式;
的通项公式;
(2)记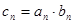 ,求数列
,求数列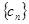 的前
的前 项和
项和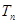 .
.
(本小题满分14分)如图,三棱柱ABC—A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3, D为AC的中点.
(1)求证:AB1//面BDC1;
(2)求二面角C1—BD—C的余弦值;
(3)在侧棱AA1上是否存在点P,使得CP⊥面BDC1?并证明你的结论.
(本小题满分12分)某学校900名学生在一次百米测试中,成绩全部介于 秒与
秒与 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组 , ,第五组
, ,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.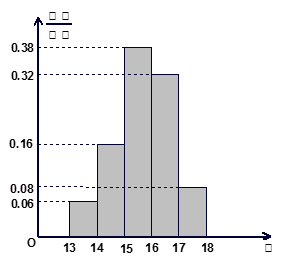
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级900名学生中,成绩属于第三组的人数;
(3)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽2个同学组成一个实验组,设其中男同学的数量为 ,求
,求 的分布列和期望.
的分布列和期望.