已知:如图,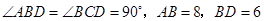 ,当
,当 为多少时,图中的两个三角形相似.
为多少时,图中的两个三角形相似.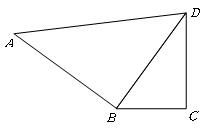
八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题:
(1)补全表格中的数据;
(2)计算两班的优秀率;
(3)计算两班的方差,并比较哪一班比较稳定?
(4)请制定比赛规则并判定哪对获胜?
在一次研究性学习活动中,李平同学看到了工人师傅在木板上画一个直角三角形,方法是(如图):画线段AB,分别以点A,B为圆心,以大于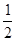 AB的长为半径画弧,两弧相交于点C,连接AC;再以点C为圆心,以AC长为半径画弧,交AC延长线于点D,连接DB.则△ABD就是直角三角形.
AB的长为半径画弧,两弧相交于点C,连接AC;再以点C为圆心,以AC长为半径画弧,交AC延长线于点D,连接DB.则△ABD就是直角三角形.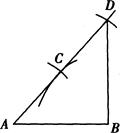
(1)请你说明工人师傅可以这么做直角三角形的理由;
(2)请利用上述方法作一个直角三角形,使其一个锐角为30°
(不写作法,保留作图痕迹).
已知一个几何体的三视图和有关的尺寸如图所示,请描述该几何体的形状,并根据图中数据计算它的表面积.
解不等式组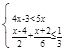 并把解在数轴上表示出来.
并把解在数轴上表示出来.
如图,在直角坐标系中,点D在y轴上,四边形ABCD是等腰梯形,AB∥CD。已知, DO⊥AB, OE⊥BC,E、O分别为垂足,BC="BO" ,O为坐标原点。
(1) 求证:DO=EO
(2) 已知:C点坐标为(4 , 8),
①求等腰梯形ABCD的腰长;
②问题探究:在这个坐标平面内是否存在点F,使以点F、D、O、E为顶点的四边形是菱形?若存在,请求出所有符合要求的F点的坐标,并说明理由;若不存在,请说明理由。