先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
(1)若x2+2y2﹣2xy+4y+4=0,求xy的值.
(2)已知整数a、b、c是不等边△ABC的三边长,满足a2+b2=6a+8b﹣25,且c是△ABC中最长的边,求c的值.
计算:
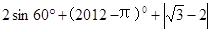
解不等式组:
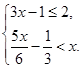
已知如图,矩形OABC的长OA=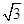 ,宽OC=1,将△AOC沿AC翻折得△AFC.
,宽OC=1,将△AOC沿AC翻折得△AFC.求过A、F、C三点的抛物线解析式;
设(1)中的抛物线与矩形OABC边CB相交于点D,与
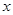 轴相交于另外一点E,若点M是
轴相交于另外一点E,若点M是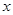 轴上的点,N是
轴上的点,N是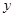 轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标若动点P以每秒
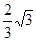 个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒
个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒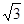 个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?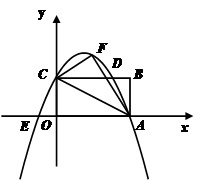
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE、OE.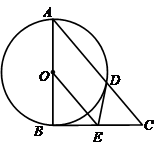
试判断DE与⊙O的位置关系并证明
求证:BC
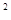 =2CD·OE;
=2CD·OE;若tanC=
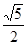 ,DE=2,求AD的长
,DE=2,求AD的长
某市自来水公司为了鼓励市民节约用水,于2012年4月开始采用以用户为单位按月分段收费办法收取水费,2012年3月底以前按原收费标准收费.两种收费标准见下表:
| 原收费标准 |
新按月分段收费标准 |
| 每吨2元 |
(1)每月用水不超过10吨(包括10吨)的用户,每吨收费1.6元; (2)每月用水超过10吨的用户,其中的10吨按每吨1.6元收费,超过10吨的部分,按每吨 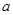 元收费( 元收费(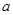 >1.6). >1.6). |
居民甲三月份、四月份各用水20吨,但四月份比三月份多交水费6元,求上表中
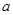 的值;
的值;若居民甲五月份用水
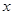 (吨),应交水费
(吨),应交水费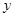 (元),求
(元),求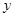 与
与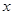 之间的函数关系式,并注明自变量x的取值范围;
之间的函数关系式,并注明自变量x的取值范围;试问居民甲五月份用水量
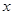 (吨)在什么范围内时,按新分段收费标准交的水费少于按原收费标准交的水费?
(吨)在什么范围内时,按新分段收费标准交的水费少于按原收费标准交的水费?
如图,已知A(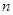 ,-2),B(1,4)是一次函数
,-2),B(1,4)是一次函数 的图象和反比例函数y=
的图象和反比例函数y= 的图象的两个交点,直线AB与
的图象的两个交点,直线AB与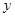 轴交于点C..
轴交于点C..
求反比例函数和一次函数的关系式;
求△AOC的面积
观察图象,直接写出不等式
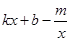 <0的解集.
<0的解集.