(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图已知四棱锥 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点 分别是
分别是 的中点.求
的中点.求
(1)异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)四棱锥 的表面积.
的表面积.
对于三次函数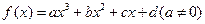 ,定义:设
,定义:设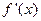 是函数
是函数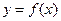 的导函数
的导函数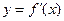 的导数,若
的导数,若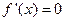 有实数解
有实数解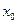 ,则称点
,则称点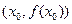 为函数
为函数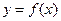 的“拐点”。现已知
的“拐点”。现已知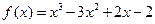 ,请解答下列问题:
,请解答下列问题:
(1)求函数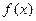 的“拐点”A的坐标;
的“拐点”A的坐标;
(2)求证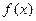 的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
已知函数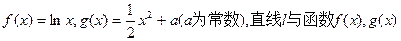 的图象都相切,且l与函数
的图象都相切,且l与函数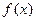 图象的切点的横坐标为1,求直线l的方程及a的值;
图象的切点的横坐标为1,求直线l的方程及a的值;
已知向量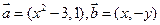 ,(其中实数
,(其中实数 和
和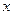 不同时为零),当
不同时为零),当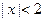 时,有
时,有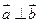 ,当
,当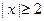 时,
时,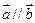 .
.
(1) 求函数式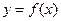 ;
;
(2)求函数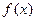 的单调递减区间;
的单调递减区间;
(3)若对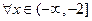
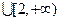 ,都有
,都有 ,求实数
,求实数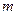 的取值范围.
的取值范围.
已知函数
(1)求函数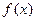 的解析式,并指出其单调性;
的解析式,并指出其单调性;
(2)函数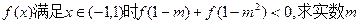 的取值集合;
的取值集合;
(3)当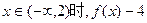 的值恰为负数,求a的取值范围。
的值恰为负数,求a的取值范围。
已知集合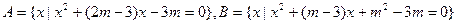 ,且满
,且满
足条件:(1)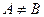 ;(2)
;(2)