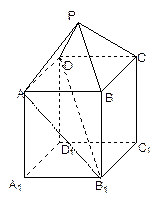已知函数 在点
在点 处取得极小值-4,使其导数
处取得极小值-4,使其导数 的
的 的取值范围为
的取值范围为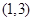 ,求:
,求:
(1) 的解析式;
的解析式;
(2)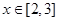 ,求
,求 的最大值;
的最大值;
已知函数 ,常数
,常数 .
.
(1)讨论函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围
的取值范围
在平面直角坐标系 ,已知圆心在第二象限、半径为
,已知圆心在第二象限、半径为 的圆C与直线y=x相切于
的圆C与直线y=x相切于
坐标原点O.椭圆 与圆C的一个交点到椭圆两焦点的距离之和为
与圆C的一个交点到椭圆两焦点的距离之和为 .
.
(1)求圆C的方程;
(2)圆C上是否存在异于原点的点Q,使 (F为椭圆右焦点),若存在,请
(F为椭圆右焦点),若存在,请
求出点Q的坐标;若不存在,请说明理由.
设平面向量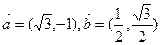 ,若存在实数
,若存在实数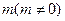 和角
和角 ,其中
,其中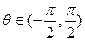 ,使向量
,使向量 ,且
,且 .
.
(1).求 的关系式;
的关系式;
(2).若 ,求
,求 的最小值,并求出此时的
的最小值,并求出此时的 值.
值.
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
…… … …
…… … ……
假设第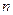 行的第二个数为
行的第二个数为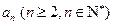 ,
,
(Ⅰ)依次写出第六行的所有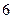 个数字;
个数字;
(Ⅱ)归纳出 的关系式并求出
的关系式并求出 的通项公式;
的通项公式;
(Ⅲ)设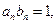 求证:
求证: …
…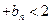
如图,在组合体中,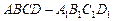 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥.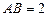 ,
,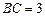 ,点
,点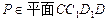 且
且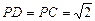 .
.
(Ⅰ)证明: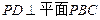 ;
;
(Ⅱ)若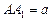 ,当
,当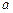 为何值时,
为何值时, .
.