(本小题满分12分)
某市文化馆在春节期间举行高中生“蓝天海洋杯”象棋比赛,规则如下:两名选手比赛时,每局胜者得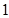 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多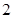 分或打满
分或打满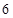 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为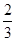 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响.
(Ⅰ)求比赛进行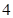 局结束,且乙比甲多得
局结束,且乙比甲多得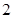 分的概率;
分的概率;
(Ⅱ)设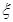 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量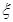 的分布列和数学期望.
的分布列和数学期望.
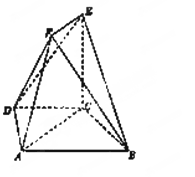
在如图所示的几何体中,四边形 是等腰梯形,
是等腰梯形,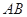 ∥
∥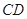 ,
,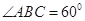 ,
,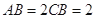 .在梯形
.在梯形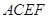 中,
中,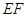 ∥
∥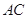 ,且
,且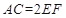 ,
,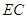 ⊥平面
⊥平面 .
.
(1)求证: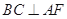 ;
;
(2)若二面角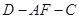 为
为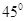 ,求
,求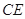 的长.
的长.
某市 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |
 |
 |
 |
 |
| 人数 |
 |
 |
 |
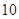 |
为了了解参加考试的学生的学习状况,该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查.
(1)问 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?
(2)从参加问卷调查的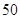 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
(3)在参加问卷调查的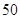 名学生中,从来自
名学生中,从来自 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用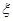 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求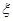 的分布列.
的分布列.
在数列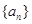 中,已知
中,已知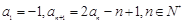 .
.
(1)求证: 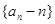 是等比数列;
是等比数列;
(2)令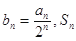 为数列
为数列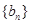 的前
的前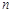 项和,求
项和,求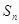 的表达式.
的表达式.
设函数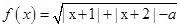 ;
;
(1)当a=5时,求函数f(x)的定义域;
(2)若函数f(x)的定义域为R,试求a的取值范围.
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: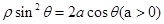 过点
过点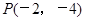 的直线
的直线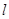 的参数方程为
的参数方程为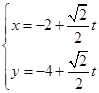 (t为参数),l与C分别交与M,N.
(t为参数),l与C分别交与M,N.
(1)写出C的平面直角坐标系方程和的普通方程;
(2)若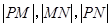 成等比数列,求a的值.
成等比数列,求a的值.