（本小题满分14分）
如图4，在三棱柱
中，△
是边长为
的等边三角形，
平面，
，
分别是
，
的中点. 
（1）求证：
∥平面
；
（2）若
为
上的动点，当
与平面
所成最大角的正切值为
时，
求平面 与平面所成二面角（锐角）的余弦值.
（本小题满分12分）
在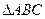
，角A，B，C的对边分别为
。
（1）判断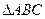的形状；
（2）若
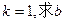的值。
（本小题满分14分）
已知曲线
在点
处的切线斜率为
（1）求
的极值；
（2）设
在（-∞，1）上是增函数，求实数
的取值范围；
（3）若数列
满足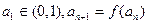
，求证：对一切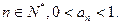
（本小题满分12分）
在平面直角坐标系
中有两定点
，
，若动点M满足
，设动点M的轨迹为C。
（1）求曲线C的方程；
（2）设直线
交曲线C于A、B两点，交直线
于点D，若
，证明：D为AB的中点。
（本小题满分12分）
已知四棱锥P—ABCD中，
平面ABCD，底面ABCD为菱形，
，AB=PA=2，E、F分别为BC、PD的中点。
（1）求证：PB//平面AFC；
（2）求平面PAE与平面PCD所成锐二面角的余弦值。
（本小题满分12分）
已知等差数列
是递增数列，且满足
（1）求数列的通项公式；
（2）令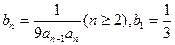
，求数列
的前
项和