已知 ,设
,设 .
.
(1)求函数 的最小正周期,并写出
的最小正周期,并写出 的减区间;
的减区间;
(2)当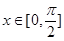 时,求函数
时,求函数 的最大值及最小值.
的最大值及最小值.

甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3道题,每人答对其中2题就停止答题,即为闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设乙答对题目的个数为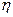 ,求
,求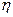 的方差;
的方差; (Ⅲ)设甲答对题目的个数为
(Ⅲ)设甲答对题目的个数为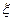 ,求
,求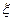 的分布列及数学期望。
的分布列及数学期望。
已知函数 在
在 内有极值,求实数
内有极值,求实数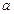 的范围。
的范围。
(本小题满分14分)设函数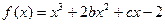 的图象与x轴相交于一点
的图象与x轴相交于一点 ,且在点
,且在点 处的切线方程是
处的切线方程是
(I)求t的值及函数 的解析式;
的解析式;
(II)设函数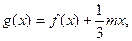
(1)若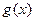 的极值存在,求实数m的取值范围。
的极值存在,求实数m的取值范围。
(2)假设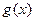 有两个极值点
有两个极值点
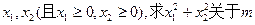 的表达式
的表达式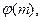 并判断
并判断 是否有最大值,若有最大值求出它;若没有最大值,说明理由。
是否有最大值,若有最大值求出它;若没有最大值,说明理由。
(本小题满分12分)
已知定义在区间上的函数 为奇函数且
为奇函数且
(1)求实数m,n的值;
(2)求证:函数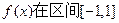 上是增函数。
上是增函数。
(3)若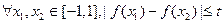 恒成立,求t的最小值。
恒成立,求t的最小值。