甲、乙两人参加某电视台举办的答题闯关游戏，按照规则，甲先从6道备选题中一次性抽取3道题独立作答，然后由乙回答剩余3道题，每人答对其中2题就停止答题，即为闯关成功。已知6道备选题中，甲能答对其中的4道题，乙答对每道题的概率都是
。（Ⅰ）求甲、乙至少有一人闯关成功的概率；
（Ⅱ）设乙答对题目的个数为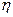
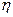，求的方差；
（Ⅲ）设甲答对题目的个数为
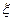，求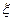的分布列及数学期望。
已知两点M（-2，0）、N（2，0），点P为坐标平面内的动点，满足|
||
|+ ·
=0，求动点P（x，y）的轨迹方程.
如图所示，过点P（2，4）作互相垂直的直线l1、l2.若l1交x轴于A，l2交y轴于B，求线段AB中点M的轨迹方程.
在R上可导的函数f(x)=
x3+
ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,求点(a,b)对应的区域的面积以及
的取值范围.
两种大小不同的钢板可按下表截成A,B,C三种规格成品:
 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
2 |
1 |
1 |
| 第二种钢板 |
1 |
2 |
3 |
某建筑工地需A，B，C三种规格的成品分别为15，18，27块，问怎样截这两种钢板，可得所需三种规格成品，且所用钢板张数最小.
某工厂生产甲、乙两种产品，计划每天每种产品的生产量不少于15吨，已知生产甲产品1吨，需煤9吨，电力4千瓦时，劳力3个；生产乙产品1吨，需煤4吨，电力5千瓦时，劳力10个；甲产品每吨的利润为7万元，乙产品每吨的利润为12万元；但每天用煤不超过300吨，电力不超过200千瓦时，劳力只有300个.问每天生产甲、乙两种产品各多少吨，才能使利润总额达到最大？