(本小题满分14分) 已知在单位圆x²+y²=1上任取一点M,作MN⊥x轴,垂足为N, 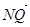 = 2
= 2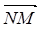 .
.
(Ⅰ)求动点Q的轨迹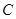 的方程;
的方程;
(Ⅱ)设点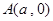 ,点
,点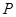 为曲线
为曲线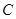 上任一点,求点
上任一点,求点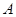 到点
到点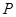 距离的最大值
距离的最大值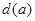 ;
;
(Ⅲ)在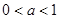 的条件下,设△
的条件下,设△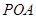 的面积为
的面积为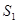 (
(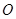 是坐标原点,
是坐标原点,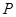 是曲线
是曲线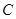 上横坐标为
上横坐标为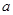 的点),以
的点),以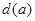 为边长的正方形的面积为
为边长的正方形的面积为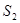 .若正数
.若正数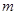 满足
满足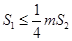 ,问
,问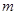 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
(本小题满分7分)选修4—2:矩阵与变换
已知矩阵M= 有特征向量
有特征向量 =
= ,
, =
= ,相应的特征值为λ1,λ2.
,相应的特征值为λ1,λ2.
(Ⅰ)求矩阵M的逆矩阵M-1及λ1,λ2;
(Ⅱ)对任意向量 =
= ,求M100
,求M100 .
.
已知 为为双曲线
为为双曲线 的两个焦点,焦距
的两个焦点,焦距 ,过左焦点
,过左焦点 垂直于
垂直于 轴的直线,与双曲线
轴的直线,与双曲线 相交于
相交于 两点,且
两点,且 为等边三角形.
为等边三角形.
(1)求双曲线 的方程;
的方程;
(2)设 为直线
为直线 上任意一点,过右焦点
上任意一点,过右焦点 作
作 的垂线交双曲线
的垂线交双曲线 与
与 两点,求证:直线
两点,求证:直线 平分线段
平分线段 (其中
(其中 为坐标原点);
为坐标原点);
(3)是否存在过右焦点 的直线
的直线 ,它与双曲线
,它与双曲线 的两条渐近线分别相交于
的两条渐近线分别相交于 两点,且使得
两点,且使得 的面积为
的面积为 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知函数 ,
, (a、b为常数).
(a、b为常数).
(1)求函数 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)当函数g(x)在x=2处取得极值-2.求函数 的解析式;
的解析式;
(3)当 时,设
时,设 ,若函数
,若函数 在定义域上存在单调减区间,求实数b的取值范围;
在定义域上存在单调减区间,求实数b的取值范围;
【改编】在如图所示的几何体中,四边形 是正方形,
是正方形, ,
, ,且
,且 ,
, ,
, .
.
(Ⅰ)若 与
与 交于点
交于点 ,求证:
,求证:  平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 与二面角
与二面角 的正切值之比.
的正切值之比.
某示范性高中的校长推荐甲、乙、丙三名学生参加某大学自主招生考核测试,在本次考核中只有合格和优秀两个等级.若考核为合格,授予10分降分资格;考核为优秀,授予20分降分资格.假设甲、乙、丙考核为优秀的概率分别为 、
、 、
、 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.
(1)求在这次考核中,甲、乙、丙三名学生至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名学生所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望.