已知 为为双曲线
为为双曲线 的两个焦点,焦距
的两个焦点,焦距 ,过左焦点
,过左焦点 垂直于
垂直于 轴的直线,与双曲线
轴的直线,与双曲线 相交于
相交于 两点,且
两点,且 为等边三角形.
为等边三角形.
(1)求双曲线 的方程;
的方程;
(2)设 为直线
为直线 上任意一点,过右焦点
上任意一点,过右焦点 作
作 的垂线交双曲线
的垂线交双曲线 与
与 两点,求证:直线
两点,求证:直线 平分线段
平分线段 (其中
(其中 为坐标原点);
为坐标原点);
(3)是否存在过右焦点 的直线
的直线 ,它与双曲线
,它与双曲线 的两条渐近线分别相交于
的两条渐近线分别相交于 两点,且使得
两点,且使得 的面积为
的面积为 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知数列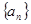 的各项全为正数,观察流程图,当
的各项全为正数,观察流程图,当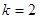 时,
时, ;当
;当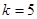 时,
时, ;
;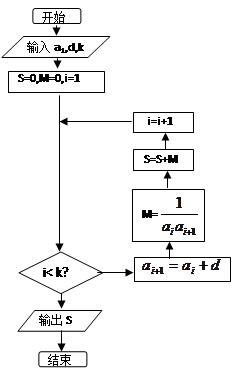
⑴写出 时,
时, 的表达式(用,
的表达式(用,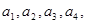 等表示);
等表示);
⑵求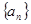 的通项公式;
的通项公式;
⑶令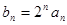 ,求
,求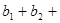
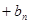 .
.
(本小题满分14分)已知函数 ,其中
,其中
(Ⅰ)求 在
在 上的单调区间;
上的单调区间;
(Ⅱ)求 在
在 (
( 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(III)对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 、
、 ,使得
,使得 是以原点
是以原点 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在 轴上?
轴上?
(本大题满分14分)
已知△ 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,
, ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合).求证直线
不重合).求证直线 与
与 轴的交点为定点,并求出该定点的坐标.
轴的交点为定点,并求出该定点的坐标.
(本小题满分13分)如图所示,四棱锥 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形, 是棱
是棱 上的动点.
上的动点.
(Ⅰ)若 是
是 的中点,求证:
的中点,求证: //平面
//平面 ;
;
(Ⅱ)若 ,求证:
,求证: ;
;
(III)在(Ⅱ)的条件下,若 ,求四棱锥
,求四棱锥 的体积.
的体积.
(本小题满分12分)在等差数列 中,
中, ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,求
的等比数列,求 的前
的前 项和
项和 .
.