如图甲所示，质量为m、电荷量为e的电子经加速电压U1，加速后，在水平方向沿O1O2垂直进入偏转电场．已知形成偏转电场的平行板电容器的极板长为L(不考虑电场边缘效应)，两极板间距为d，O1O2为两极板的中线，P是足够大的荧光屏，且屏与极板右边缘的距离也为L．求：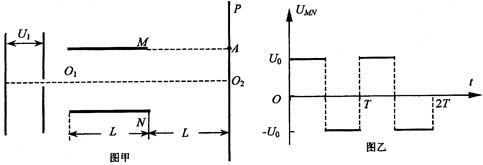
(1)粒子进入偏转电场的速度v的大小；
(2)若偏转电场两板间加恒定电压，电子经过偏转电场后正好打中屏上的A点，A点与极板M在同一水平线上，求偏转电场所加电压U2；
(3)若偏转电场两板间的电压按如图乙所示作周期性变化，要使电子经加速电场后在t=0 时刻进入偏转电场后水平击中A点，试确定偏转电场电压U0以及周期T分别应该满足的条件．
A、B两列火车在同一轨道上通向行驶，A车在前，速度为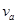
=10m/s,B车在后速度为
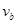=30m/s因大雾能见度低，B车在距A车600m时，才发现前方有A车，这时B车立即刹车，但要经过180m的距离B车才能停止。问
（1）B车刹车时的加速度大小为多少？
（2）A车若按原速前进，两车是否相撞，若会相撞，将在何时何地发生？
（3）B车在刹车的同时发出信号，A车在司机受到信号2s后加速前进，求A车的加速度满足什么条件才能避免事故发生？（不计信号传输时间）
跳伞运动员做低空跳伞表演，飞机离地面224m水平飞行，运动员离开飞机在竖直方向做自由落体运动；经过一段时间后，立即打开降落伞，展开伞后运动员以12.5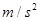
的加速度在竖直方向上匀减速下降，为了运动员的安全，要求运动员落地时竖直方向的速度最大不超过5m/s,(g=10)
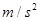(1)运动员展开伞时，离地面的高度至少多少？
（2）运动员在空中的最短时间是多少？
一物体由斜面顶端由静止开始匀加速下滑，最初的3s内的位移为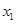
，最后3s内的位移为
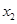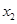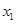，若-=6米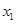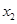，：=3:7，求斜面的长度为多少？
一物体做匀减速直线运动，初速度是3m/s加速度大小为0.4
,在某1s内它通过的位移为0.4m,那么在这1s之前物体已运动了多少时间？
为测量一个高楼的高度，某同学设计了如下实验：在一根长为L的绳两端各栓一重球，一人站在楼顶上，手执上端的重球让下端重球以楼面等高悬于楼顶边沿，将重球无初速度释放，另一人在楼下测量两球落地的时间差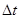
，即可根据L、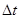、g得出高楼的高度（不计空气阻力和球的大小）。
1）从原理上讲，这个方案是否正确：_________(填“正确”或“不正确”)请陈述理由_________________________________________________________________
2)从实际测量来看，你估计最大的困难是_____________________________________