如图，在Rt△ABC中，∠ACB=90°，AC=6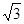
cm ，BC=6cm，经过A，B的直线l以1cm/秒的速度向下作匀速平移运动，交BC于点B′，交CD于点 D′，与此同时，点P从点B′ 出发，在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动．设它们运动的时间为t秒．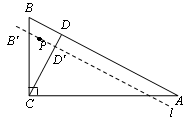
（1）你求出的AB的长是 ；
（2）过点C作CD⊥AB于点D，t为何值时，点P移动到CD上？
（3）t为何值时，以点P为圆心、1cm为半径的圆与直线CD相切？
（4）以点P为圆心、1 cm为半径的⊙P与CD所在的直线相交时，是否存在点P与两个交点构成的三角形是等边三角形？若存在，直接写出t的值；若不存在，说明理由.
已知：如图，
中，
，
于
，
于
，
与
相交于点
．求证：
；
已知
是一元二次方程
的实数根，求代数式
的值.
计算: 
．在Rt△ABC中，∠ACB=90°，tan∠BAC=
. 点D在边AC上（不与A，C重合），连结BD，F为BD中点.
（1）若过点D作DE⊥AB于E，连结CF、EF、CE，如图1． 设
，则k ="" ；
（2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示．求证：BE-DE=2CF；
（3）若BC=6，点D在边AC的三等分点处，将线段AD绕点A旋转，点F始终为BD中点，求线段CF长度的最大值．
．已知平面直角坐标系xOy中, 抛物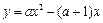线
与直线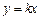
的一个公共点为
.
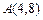（1）求此抛物线和直线的解析式；
（2）若点P在线段OA上，过点P作y轴的平行线交（1）中抛物线于点Q，求线段PQ长度的最大值；
（3）记（1）中抛物线的顶点为M，点N在此抛物线上，若四边形AOMN恰好是梯形，求点N的坐标及梯形AOMN的面积.