已知p: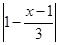 ≤2; q:
≤2; q: ≤0(m>0),若
≤0(m>0),若 是
是 的充分而不必要条件,求实数m的取值范围.
的充分而不必要条件,求实数m的取值范围.
曲线 都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线
都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线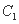 的短轴,并且是曲线
的短轴,并且是曲线 的长轴 . 直线
的长轴 . 直线 与曲线
与曲线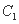 交于A,D两点(A在D的左侧),与曲线
交于A,D两点(A在D的左侧),与曲线 交于B,C两点(B在C的左侧).
交于B,C两点(B在C的左侧).
(1)当 =
= ,
, 时,求椭圆
时,求椭圆 的方程;
的方程;
(2)若 ,求
,求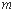 的值.
的值.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得,已知FA⊥平面ABC,AB=2,BD=1,AF=2, CE=3,O为AB的中点.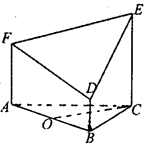
(1)求证:OC⊥DF;
(2)求平面DEF与平面ABC相交所成锐二面角的大小;
(3)求多面体ABC—FDE的体积V.
甲、乙、丙三人独立参加某企业的招聘考试,根据三人的专业知识、应试表现、工作经验等综合因素,三人被招聘的概率依次为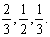 用
用 表示被招聘的人数。
表示被招聘的人数。
(1)求三人中至少有一人被招聘的概率;
(2)求随机变量 的分布列和数学期望。
的分布列和数学期望。
已知函数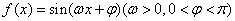 的一系列对应值如表:
的一系列对应值如表:
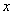 |
 |
 |
 |
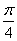 |
 |
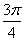 |
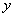 |
 |
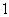 |
 |
 |
 |
 |
(1)求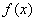 的解析式;
的解析式;
(2)若在 中,
中,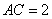 ,
,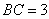 ,
,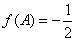 (A为锐角),求
(A为锐角),求 的面积.
的面积.
已知函数 ,(
,( 为实常数)
为实常数)
(1)若 ,将
,将 写出分段函数的形式,并画出简图,指出其单调递减区间;
写出分段函数的形式,并画出简图,指出其单调递减区间;
(2)设 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的表达式。
的表达式。