曲线 都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线
都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线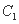 的短轴,并且是曲线
的短轴,并且是曲线 的长轴 . 直线
的长轴 . 直线 与曲线
与曲线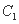 交于A,D两点(A在D的左侧),与曲线
交于A,D两点(A在D的左侧),与曲线 交于B,C两点(B在C的左侧).
交于B,C两点(B在C的左侧).
(1)当 =
= ,
, 时,求椭圆
时,求椭圆 的方程;
的方程;
(2)若 ,求
,求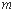 的值.
的值.
若某产品的直径长与标准值的差的绝对值不超过
时,则视为合格品,否则视为不合格品。在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取
件进行检测,结果发现有
件不合格品。计算这
件不合格品的直径长与标准值的差(单位:
), 将所得数据分组,得到如下频率分布表:
| 分组 |
频数 |
频率 |
| [-3, -2) |
0.10 |
|
| [-2, -1) |
8 |
|
| (1,2] |
0.50 |
|
| (2,3] |
10 |
|
| (3,4] |
||
| 合计 |
50 |
1.00 |
(Ⅰ)将上面表格中缺少的数据填在相应位置;
(Ⅱ)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(Ⅲ)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
设定义在( )上的函数
(Ⅰ)求
的最小值;
(Ⅱ)若曲线
在点
处的切线方程为
,求
的值。
设△ 的内角 所对边的长分别为 ,且有 .
(Ⅰ)求角
的大小;
(Ⅱ)若
为
的中点,求
的长.
若函数
满足
(1)
;
(2)对任意
,有
;
(3)在(0,1)上单调递减。则称
为补函数。已知函数
.
(1)判函数
是否为补函数,并证明你的结论;
(2)若存在
,使得
,若
是函数
的中介元,记
时
的中介元为
,且
,若对任意的
,都有
,求
的取值范围;
(3)当
,
时,函数
的图像总在直线
的上方,求P的取值范围。
已知三点
,曲线
上任意一点
满足
.
(1)求曲线
的方程;
(2)动点
在曲线
上,曲线
在点
处的切线为
,问:是否存在定点
,使得
与
都不相交,交点分别为
,且
与
的面积之比是常数?若存在,求
的值。若不存在,说明理由。