两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.
求:1)d的变化范围;
2)当d取最大值时两条直线的方程.
如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求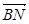 的长; (2)求cos<
的长; (2)求cos< >的值;(3)求证:A1B⊥C1M.
>的值;(3)求证:A1B⊥C1M.
(本小题满分12分)
(1)焦点在x轴上的椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
(2)已知双曲线的一条渐近线方程是 ,并经过点
,并经过点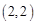 ,求此双曲线的标准方程.
,求此双曲线的标准方程.
(本小题满分12分)设直线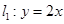 与直线
与直线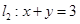 交于
交于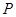 点.
点.
(1)当直线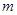 过
过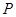 点,且与直线
点,且与直线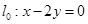 垂直时,求直线
垂直时,求直线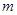 的方程;
的方程;
(2)当直线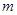 过
过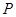 点,且坐标原点
点,且坐标原点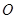 到直线
到直线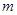 的距离为
的距离为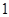 时,求直线
时,求直线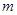 的方程.
的方程.
(本小题满分14分)已知函数 处取得极值2。
处取得极值2。
(Ⅰ) 求函数
求函数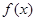 的表达式;
的表达式;
(Ⅱ)当 满足什么条件时,函数
满足什么条件时,函数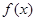 在区间
在区间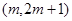 上单调递增?
上单调递增?
(Ⅲ)若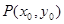 为
为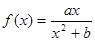 图象上任意一点,直线与
图象上任意一点,直线与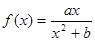 的图象切于点P,求直线的斜率
的图象切于点P,求直线的斜率 的取值范围
的取值范围
(本小题满分12分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第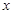 个月的利润
个月的利润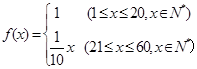 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第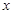 个月的当月利润率
个月的当月利润率 ,例如:
,例如: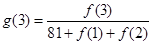 .
.
(Ⅰ) 求
求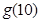 ;(Ⅱ)求第
;(Ⅱ)求第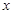 个月的当月利润率
个月的当月利润率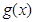 ;
;
(Ⅲ)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.