已知双曲线
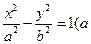 >0,b>0),的一个焦点是
>0,b>0),的一个焦点是 ,离心率
,离心率 ,
,
(1)求双曲线 的方程
的方程
(2)若以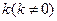 为斜率的直线
为斜率的直线 与双曲线
与双曲线 交于两个不同的点
交于两个不同的点 ,线 段
,线 段 的垂直平分线与两坐标轴围成的三角形的面积为4,求实数
的垂直平分线与两坐标轴围成的三角形的面积为4,求实数 的取值范围.
的取值范围.
. 已知 ,
, ,动点
,动点 满足
满足 .
.
(1)求动点 的轨迹方程.
的轨迹方程.
(2)设动点 的轨迹方程与直线
的轨迹方程与直线 交于
交于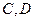 两点,
两点,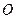 为坐标原点求证:
为坐标原点求证:
已知椭圆 及直线
及直线 .
.
(1)当直线与椭圆有公共点时,求实数 的取值范围.
的取值范围.
(2)求被椭圆截得的最长弦所在直线方程.
求以椭圆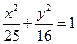 的顶点为焦点,焦点为顶点的双曲线方程,并求出其离心率.
的顶点为焦点,焦点为顶点的双曲线方程,并求出其离心率.
(提示:1、12、13、14班同学请完成试题(B),其他班级同学任选试题(A)或(B)作答)
(A) 已知点A(2,3),B(5,4),C(7,10)及 ,试问:
,试问:
(1)t为何值时,P在第三象限?
(2)是否存在D点使得四边形ABCD为平行四边形,若存在,求出D点坐标.
(B) 已知平行四边形ABCD,对角线AC与BD交于点E,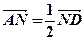 ,连接BN交AC于M,
,连接BN交AC于M,
(1)若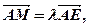 求实数λ.
求实数λ.
(2)若B(0,0),C(1,0),D(2,1),求M的坐标