已知函数
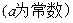
(1)是否存在实数 ,使函数
,使函数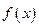 是
是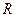 上的奇函数,若不存在,说明理由,若存在实数
上的奇函数,若不存在,说明理由,若存在实数 ,求函数
,求函数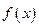 的值域;
的值域;
(2)探索函数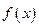 的单调性
的单调性 ,并利用定义加以证明。
,并利用定义加以证明。
二次函数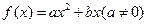 ,满足
,满足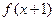 为偶函数,且方程
为偶函数,且方程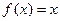 有相等实根。
有相等实根。
(1)求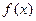 的解析式;
的解析式;
(2)求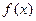 在
在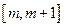 上的最大值。
上的最大值。
某商家经销一种销售成本 为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
(1)设销售单价为每千克x元,月销售利润 为y元,求y与x的函数关系式;
为y元,求y与x的函数关系式;
商店想在月销售成本不超过10000元的情况下,使得月销售利润不少于8000元,销售单价应定为多少元时,利润最大?
已知函数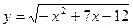 的定义域是
的定义域是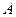 ,函数
,函数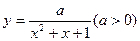 在
在 上的值域为
上的值域为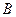 ,全集为
,全集为 ,且
,且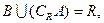 求实数
求实数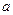 的取值范围。
的取值范围。
(1)画出函数 的图象并指出单调区间;
的图象并指出单调区间;
(2)利用图象讨论:
关于 方程
方程 (
( 为常数)解的个数?
为常数)解的个数?