(本小题12分)如图所示,三棱柱A1B1C1—ABC的三视图中,正(主)视图和侧(左)视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.
已知 ,点
,点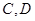 依次满足
依次满足 。
。
(1)求点 的轨迹;
的轨迹;
(2)过点 作直线
作直线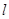 交以
交以 为焦点的椭圆于
为焦点的椭圆于 两点,线段
两点,线段 的中点到
的中点到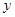 轴的距离为
轴的距离为 ,且直线
,且直线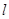 与点
与点 的轨迹相切,求该椭圆的方程;
的轨迹相切,求该椭圆的方程;
(3)在(2)的条件下,设点 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点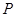 及以
及以 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线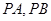 都相切,如存在,求出
都相切,如存在,求出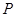 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.
据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为
 .现已知相距18
.现已知相距18 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设 (
( ).
).
(1)试将 表示为
表示为 的函数; (2)若
的函数; (2)若 ,且
,且 时,
时, 取得最小值,试求
取得最小值,试求 的值.
的值.
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB=EF.
(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
在 中,角
中,角 所对的边分别为
所对的边分别为 。已知
。已知 ,
, .
.
(1)若 ,求
,求 的面积; (2)求
的面积; (2)求 的值.
的值.
如果函数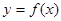 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意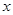 ,存在实数
,存在实数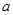 使得
使得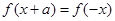 成立,则称此函数具有“
成立,则称此函数具有“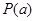 性质”。
性质”。
(1)判断函数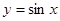 是否具有“
是否具有“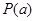 性质”,若具有“
性质”,若具有“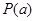 性质”,求出所有
性质”,求出所有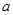 的值;若不具有“
的值;若不具有“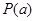 性质”,说明理由;
性质”,说明理由;
(2)已知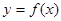 具有“
具有“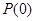 性质”,且当
性质”,且当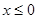 时
时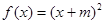 ,求
,求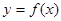 在
在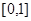 上有最大值;
上有最大值;
(3)设函数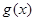 具有“
具有“ 性质”,且当
性质”,且当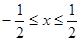 时,
时,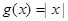 .若
.若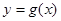 与
与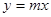 交点个数为2013,求
交点个数为2013,求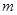 的值.
的值.