古运河是扬州的母亲河,为打造古运河风光带,现有一段河道整治任务由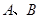 两工程队完成.
两工程队完成.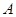 工程队单独整治该河道要16天才能完成;
工程队单独整治该河道要16天才能完成; 工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,问A工程队一共做了多少天?
工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,问A工程队一共做了多少天?
(1)根据题意,万颖、刘寅两名同学分别列出尚不完整的方程如下:
万颖: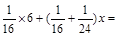

刘寅: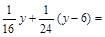 1
1
根据万颖、刘寅两名同学所列的方程,请你分别指出未知数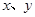 表示的意义,然后在,然后在方框中补全万颖同学所列的方程:
表示的意义,然后在,然后在方框中补全万颖同学所列的方程:
万颖: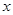 表示________________,刘寅:
表示________________,刘寅: 表示________________,万颖同学所列不完整的方程中的方框内该填 .
表示________________,万颖同学所列不完整的方程中的方框内该填 .
(2)求A工程队一共做了多少天.(写出完整的解答过程)
小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.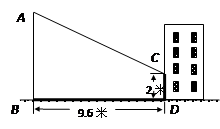
如图,在正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
(1)以点O(0,0)为位似中心,按比例尺3:1在位似中心的同侧将△OAB放大为△OA’B’,放大后点A、B的对应点分别为A’、B’ .画出△OA’B’,并写出点A’、B’的坐标:A’(),B’().
(2)在(1)中,若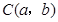 为线段
为线段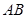 上任一点,写出变化后点
上任一点,写出变化后点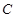 的对应点
的对应点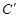 的坐标 ().
的坐标 ().
已知,如图,抛物线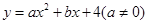 与
与 轴交于点
轴交于点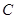 ,与
,与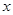 轴交于点
轴交于点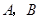 ,点
,点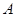 的坐标为
的坐标为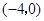 ,对称轴是
,对称轴是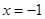 .
.
(1)求该抛物线的解析式;
(2)点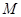 是线段
是线段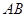 上的动点,过点
上的动点,过点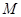 作
作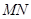 ∥
∥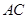 ,分别交
,分别交 轴、
轴、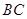 于点P、
于点P、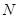 ,连接
,连接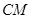 .当
.当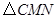 的面积最大时,求点
的面积最大时,求点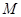 的坐标;
的坐标;
(3)在(2)的条件下,求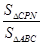 的值.
的值.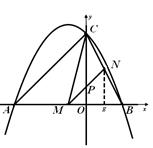
已知:如图,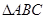 内接于⊙O,
内接于⊙O, 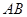 为⊙O的直径,
为⊙O的直径,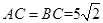 , 点
, 点 是
是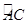 上一个动点,连结
上一个动点,连结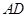 、
、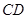 和
和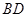 ,
, 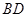 与
与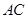 相交于点
相交于点 , 过点
, 过点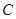 作
作 于
于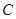 ,
,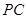 与
与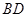 相交于点
相交于点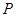 ,连结
,连结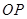 和
和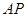 .
.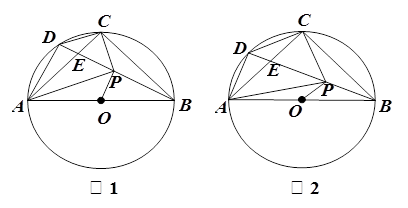
(1)求证: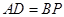 ;
;
(2)如图1,若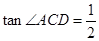 , 求证:
, 求证: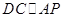 ;
;
(3) 如图2,设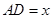 , 四边形
, 四边形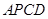 的面积为
的面积为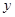 ,求
,求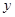 与
与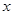 之间的关系式.
之间的关系式.
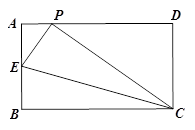
已知:如图,矩形ABCD中, 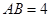 ,
,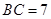 ,点P是AD边上一个动点,
,点P是AD边上一个动点,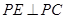 ,
, 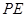 交
交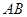 于点
于点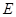 ,对应点
,对应点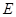 也随之在
也随之在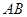 上运动,连结
上运动,连结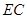 .
.
(1)若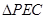 是等腰三角形,求
是等腰三角形,求 的长;
的长;
(2)当 时,求
时,求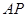 的长.
的长.